Question Number 40700 by Necxx last updated on 26/Jul/18
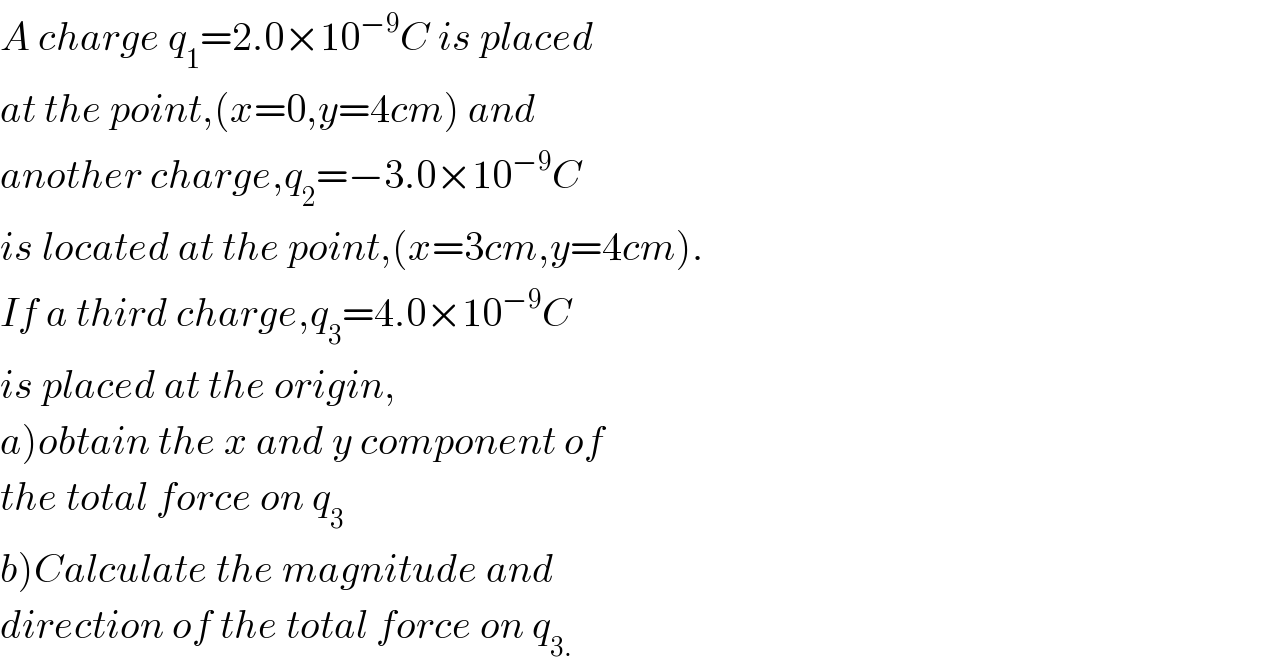
$${A}\:{charge}\:{q}_{\mathrm{1}} =\mathrm{2}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} {C}\:{is}\:{placed} \\ $$$${at}\:{the}\:{point},\left({x}=\mathrm{0},{y}=\mathrm{4}{cm}\right)\:{and} \\ $$$${another}\:{charge},{q}_{\mathrm{2}} =−\mathrm{3}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} {C} \\ $$$${is}\:{located}\:{at}\:{the}\:{point},\left({x}=\mathrm{3}{cm},{y}=\mathrm{4}{cm}\right). \\ $$$${If}\:{a}\:{third}\:{charge},{q}_{\mathrm{3}} =\mathrm{4}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} {C} \\ $$$${is}\:{placed}\:{at}\:{the}\:{origin}, \\ $$$$\left.{a}\right){obtain}\:{the}\:{x}\:{and}\:{y}\:{component}\:{of} \\ $$$${the}\:{total}\:{force}\:{on}\:{q}_{\mathrm{3}} \\ $$$$\left.{b}\right){Calculate}\:{the}\:{magnitude}\:{and} \\ $$$${direction}\:{of}\:{the}\:{total}\:{force}\:{on}\:{q}_{\mathrm{3}.} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Jul/18
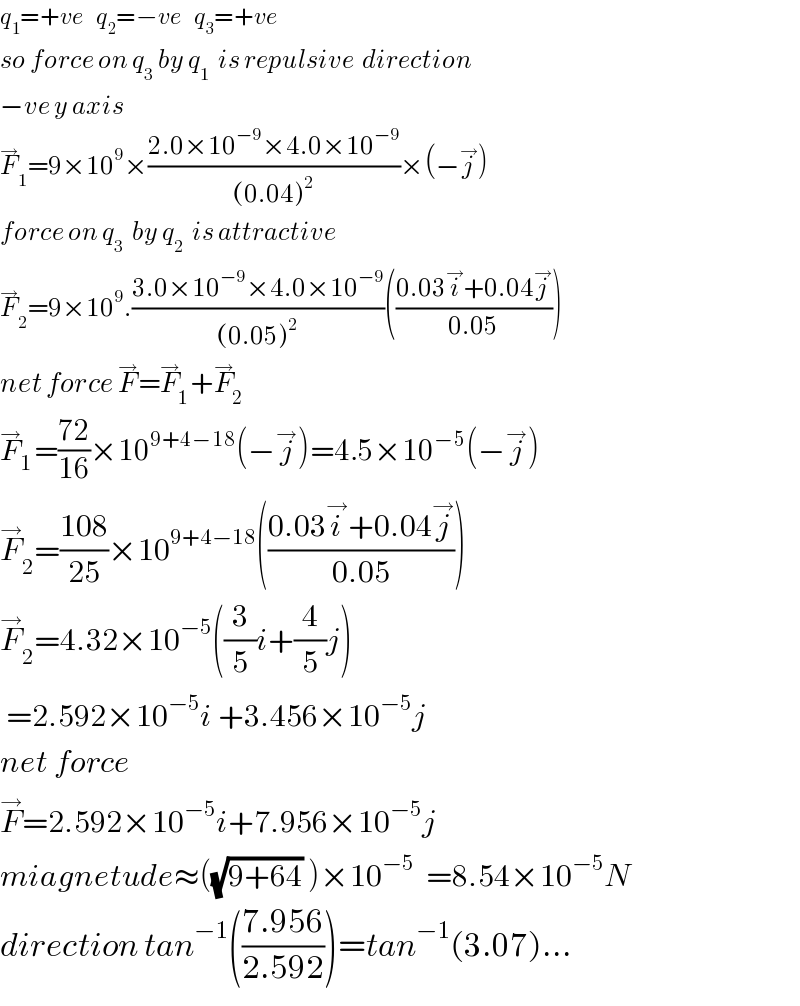
$${q}_{\mathrm{1}} =+{ve}\:\:\:{q}_{\mathrm{2}} =−{ve}\:\:\:{q}_{\mathrm{3}} =+{ve} \\ $$$${so}\:{force}\:{on}\:{q}_{\mathrm{3}} \:{by}\:{q}_{\mathrm{1}} \:\:{is}\:{repulsive}\:\:{direction} \\ $$$$−{ve}\:{y}\:{axis} \\ $$$$\overset{\rightarrow} {{F}}_{\mathrm{1}} =\mathrm{9}×\mathrm{10}^{\mathrm{9}} ×\frac{\mathrm{2}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} ×\mathrm{4}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} }{\left(\mathrm{0}.\mathrm{04}\right)^{\mathrm{2}} }×\left(−\overset{\rightarrow} {{j}}\right) \\ $$$${force}\:{on}\:{q}_{\mathrm{3}} \:\:{by}\:{q}_{\mathrm{2}} \:\:{is}\:{attractive} \\ $$$$\overset{\rightarrow} {{F}}_{\mathrm{2}} =\mathrm{9}×\mathrm{10}^{\mathrm{9}} .\frac{\mathrm{3}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} ×\mathrm{4}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} }{\left(\mathrm{0}.\mathrm{05}\right)^{\mathrm{2}} }\left(\frac{\mathrm{0}.\mathrm{03}\overset{\rightarrow} {{i}}+\mathrm{0}.\mathrm{04}\overset{\rightarrow} {{j}}}{\mathrm{0}.\mathrm{05}}\right) \\ $$$${net}\:{force}\:\overset{\rightarrow} {{F}}=\overset{\rightarrow} {{F}}_{\mathrm{1}} +\overset{\rightarrow} {{F}}_{\mathrm{2}} \\ $$$$\overset{\rightarrow} {{F}}_{\mathrm{1}} =\frac{\mathrm{72}}{\mathrm{16}}×\mathrm{10}^{\mathrm{9}+\mathrm{4}−\mathrm{18}} \left(−\overset{\rightarrow} {{j}}\right)=\mathrm{4}.\mathrm{5}×\mathrm{10}^{−\mathrm{5}} \left(−\overset{\rightarrow} {{j}}\right) \\ $$$$\overset{\rightarrow} {{F}}_{\mathrm{2}} =\frac{\mathrm{108}}{\mathrm{25}}×\mathrm{10}^{\mathrm{9}+\mathrm{4}−\mathrm{18}} \left(\frac{\mathrm{0}.\mathrm{03}\overset{\rightarrow} {{i}}+\mathrm{0}.\mathrm{04}\overset{\rightarrow} {{j}}}{\mathrm{0}.\mathrm{05}}\right) \\ $$$$\overset{\rightarrow} {{F}}_{\mathrm{2}} =\mathrm{4}.\mathrm{32}×\mathrm{10}^{−\mathrm{5}} \left(\frac{\mathrm{3}}{\mathrm{5}}{i}+\frac{\mathrm{4}}{\mathrm{5}}{j}\right) \\ $$$$\:=\mathrm{2}.\mathrm{592}×\mathrm{10}^{−\mathrm{5}} {i}\:+\mathrm{3}.\mathrm{456}×\mathrm{10}^{−\mathrm{5}} {j} \\ $$$${net}\:{force} \\ $$$$\overset{\rightarrow} {{F}}=\mathrm{2}.\mathrm{592}×\mathrm{10}^{−\mathrm{5}} {i}+\mathrm{7}.\mathrm{956}×\mathrm{10}^{−\mathrm{5}} {j} \\ $$$${miagnetude}\approx\left(\sqrt{\mathrm{9}+\mathrm{64}}\:\right)×\mathrm{10}^{−\mathrm{5}} \:\:=\mathrm{8}.\mathrm{54}×\mathrm{10}^{−\mathrm{5}} {N} \\ $$$${direction}\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{7}.\mathrm{956}}{\mathrm{2}.\mathrm{592}}\right)={tan}^{−\mathrm{1}} \left(\mathrm{3}.\mathrm{07}\right)… \\ $$
