Question Number 111734 by Aina Samuel Temidayo last updated on 04/Sep/20
$$\mathrm{A}\:\mathrm{chord}\:\mathrm{which}\:\mathrm{is}\:\mathrm{a}\:\mathrm{perpendicular} \\ $$$$\mathrm{bisector}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{length}\:\mathrm{18cm}\:\mathrm{in}\:\mathrm{a} \\ $$$$\mathrm{circle},\:\mathrm{has}\:\mathrm{length}. \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 04/Sep/20
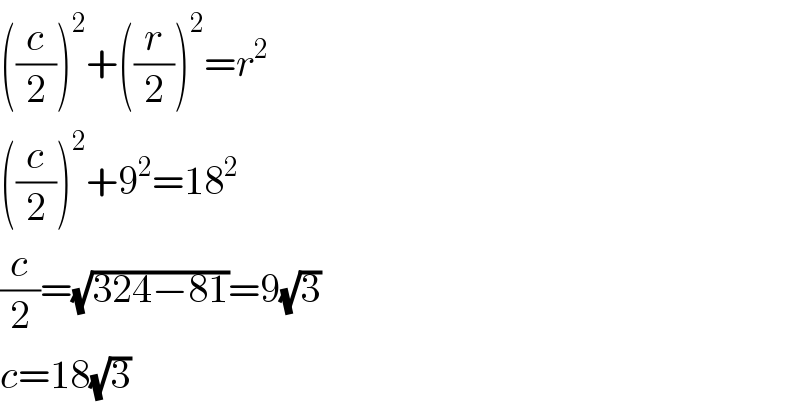
$$\left(\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{r}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\frac{{c}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} =\mathrm{18}^{\mathrm{2}} \\ $$$$\frac{{c}}{\mathrm{2}}=\sqrt{\mathrm{324}−\mathrm{81}}=\mathrm{9}\sqrt{\mathrm{3}} \\ $$$${c}=\mathrm{18}\sqrt{\mathrm{3}} \\ $$
Commented by Aina Samuel Temidayo last updated on 04/Sep/20

$$\mathrm{Diagram}\:\mathrm{please}\overset{} {?} \\ $$
Commented by prakash jain last updated on 05/Sep/20
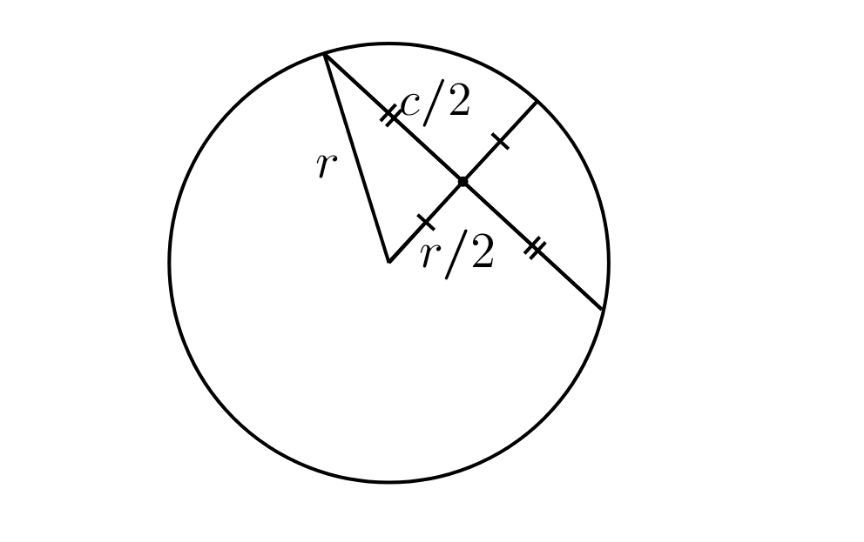
Commented by Aina Samuel Temidayo last updated on 05/Sep/20

$$\mathrm{Please}\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{know}\:\mathrm{the}\:\mathrm{chord}\:\mathrm{is} \\ $$$$\mathrm{also}\:\mathrm{bisected}? \\ $$
Commented by prakash jain last updated on 05/Sep/20

$$\mathrm{Radius}\:\mathrm{is}\:\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{chord} \\ $$$$\mathrm{and}\:\mathrm{perpendicular}\:\mathrm{radius}\:\mathrm{always} \\ $$$$\mathrm{bisects}\:\mathrm{chord} \\ $$
Commented by Aina Samuel Temidayo last updated on 05/Sep/20

$$\mathrm{Ok}.\:\mathrm{Thanks}. \\ $$
Commented by Rasheed.Sindhi last updated on 05/Sep/20
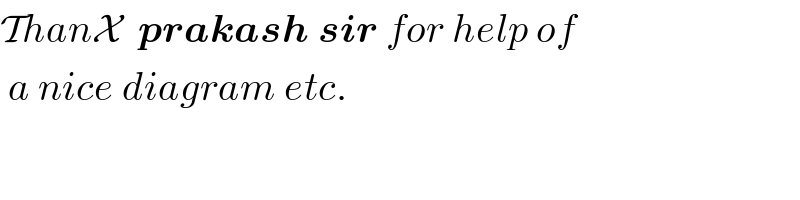
$$\mathcal{T}{han}\mathcal{X}\:\:\boldsymbol{{prakash}}\:\boldsymbol{{sir}}\:{for}\:{help}\:{of} \\ $$$$\:{a}\:{nice}\:{diagram}\:{etc}. \\ $$
