Menu Close

A-cirlce-is-drawn-to-touch-the-sides-of-a-triangle-whose-sides-are-12cm-10cm-and-9cm-Find-the-radius-of-the-circle-

Tinku Tara 0 Comments
Pin




Question Number 16014 by chux last updated on 16/Jun/17
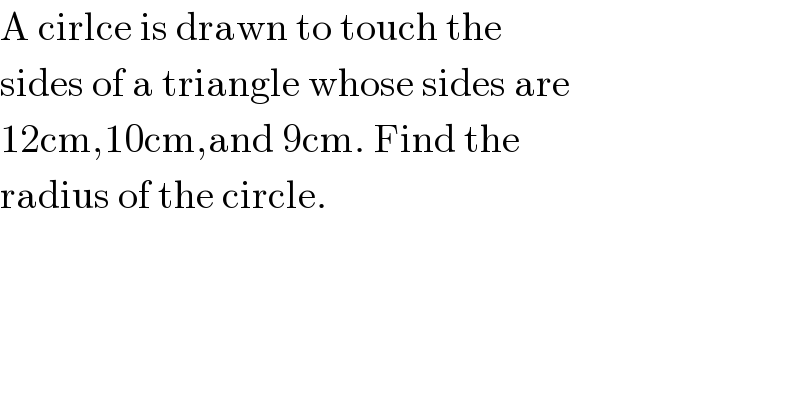
A cirlce is drawn to touch the sides of a triangle whose sides are 12cm,10cm,and 9cm. Find the radius of the circle.
$$\mathrm{A}\:\mathrm{cirlce}\:\mathrm{is}\:\mathrm{drawn}\:\mathrm{to}\:\mathrm{touch}\:\mathrm{the} \\ $$$$\mathrm{sides}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{whose}\:\mathrm{sides}\:\mathrm{are} \\ $$$$\mathrm{12cm},\mathrm{10cm},\mathrm{and}\:\mathrm{9cm}.\:\mathrm{Find}\:\mathrm{the}\: \\ $$$$\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}. \\ $$
Answered by RasheedSoomro last updated on 16/Jun/17
The circle which touches the sides of a triangle is called in-circle and its radius is called in-radius. in-radius (r) is determined by the formula below: r=(△/s) If a, b and c are the sides of the triangle: s=(a+b+c)/2 s: semi-perimeter △=(√(s(s−a)(s−b)(s−c))) △: area of the triangle We are given a=12cm,b=10cm,c=9cm So s=(12+10+9)/2=15.5 and △=(√(15.5(15.5−12)(15.5−10)(15.5−9))) =(√(15.5×3.5×5.5×6.5))≈44.04 Now the in-radius is r=(△/s)=((44.04)/(15.5))=2.84 cm
$$\mathrm{The}\:\mathrm{circle}\:\mathrm{which}\:\mathrm{touches}\:\mathrm{the}\:\mathrm{sides} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{is}\:\mathrm{called}\:\boldsymbol{\mathrm{in}}-\boldsymbol{\mathrm{circle}}\:\mathrm{and} \\ $$$$\mathrm{its}\:\mathrm{radius}\:\mathrm{is}\:\mathrm{called}\:\boldsymbol{\mathrm{in}}-\boldsymbol{\mathrm{radius}}.\: \\ $$$$\mathrm{in}-\mathrm{radius}\:\left(\mathrm{r}\right)\:\mathrm{is}\:\mathrm{determined} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{below}: \\ $$$$\:\:\:\:\:\:\mathrm{r}=\frac{\bigtriangleup}{\mathrm{s}} \\ $$$$\mathrm{If}\:\mathrm{a},\:\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{are}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{triangle}: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{s}=\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)/\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{s}:\:\mathrm{semi}-\mathrm{perimeter} \\ $$$$\:\:\:\:\bigtriangleup=\sqrt{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)}\:\:\:\:\bigtriangleup:\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle} \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{are}\:\mathrm{given}\:\mathrm{a}=\mathrm{12cm},\mathrm{b}=\mathrm{10cm},\mathrm{c}=\mathrm{9cm} \\ $$$$\mathrm{So}\:\:\:\:\:\:\:\:\:\mathrm{s}=\left(\mathrm{12}+\mathrm{10}+\mathrm{9}\right)/\mathrm{2}=\mathrm{15}.\mathrm{5} \\ $$$$\:\mathrm{and}\:\bigtriangleup=\sqrt{\mathrm{15}.\mathrm{5}\left(\mathrm{15}.\mathrm{5}−\mathrm{12}\right)\left(\mathrm{15}.\mathrm{5}−\mathrm{10}\right)\left(\mathrm{15}.\mathrm{5}−\mathrm{9}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{15}.\mathrm{5}×\mathrm{3}.\mathrm{5}×\mathrm{5}.\mathrm{5}×\mathrm{6}.\mathrm{5}}\approx\mathrm{44}.\mathrm{04} \\ $$$$\mathrm{Now}\:\mathrm{the}\:\mathrm{in}-\mathrm{radius}\:\mathrm{is} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{r}=\frac{\bigtriangleup}{\mathrm{s}}=\frac{\mathrm{44}.\mathrm{04}}{\mathrm{15}.\mathrm{5}}=\mathrm{2}.\mathrm{84}\:\mathrm{cm} \\ $$
Commented by chux last updated on 16/Jun/17
thanks sir.
$$\mathrm{thanks}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *