A-cord-is-drawn-at-random-in-a-given-circle-Whats-the-probability-p-that-the-cord-is-longer-than-the-side-of-an-inscribed-equilateral-triangle-in-the-circle-

Question Number 60000 by malwaan last updated on 16/May/19

A c o r d i s d r a w n a t r a n d o m

i n a g i v e n c i r c l e .

W h a t s t h e p r o b a b i l i t y p t h a t

t h e c o r d i s l o n g e r t h a n t h e s i d e

o f a n i n s c r i b e d e q u i l a t e r a l

t r i a n g l e i n t h e c i r c l e ?

Commented by mr W last updated on 16/May/19

\frac{1}{3}

Commented by MJS last updated on 17/May/19

this is called Bertrand paradoxon . dependent

on the chosen method of randomization

we get p = 1 / 2, 1 / 3 or 1 / 4 . look it up!

Commented by malwaan last updated on 17/May/19

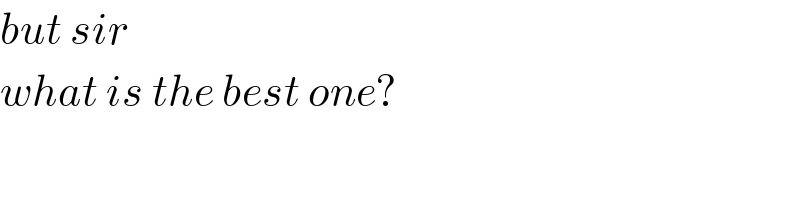
b u t s i r

w h a t i s t h e b e s t o n e ?

Commented by mr W last updated on 17/May/19

https://en.m.wikipedia.org/wiki/Bertrand_paradox_(probability)

Commented by MJS last updated on 17/May/19

{there}^{'} s no best one . we cannot give an

answer . {it}^{'} s undefined .

Commented by mr W last updated on 17/May/19

I t h i n k t h e q u e s t i o n i s d e f i n e d i f i t i s :

T w o p o i n t s A a n d B a r e c h o o s e n a t

r a n d o m o n a g i v e n c i r c l e .

W h a t i s t h e p r o b a b i l i t y t h a t t h e c o r d

A B i s l o n g e r t h a n l w i t h 0 < l < d i a m e t e r .

Commented by MJS last updated on 17/May/19

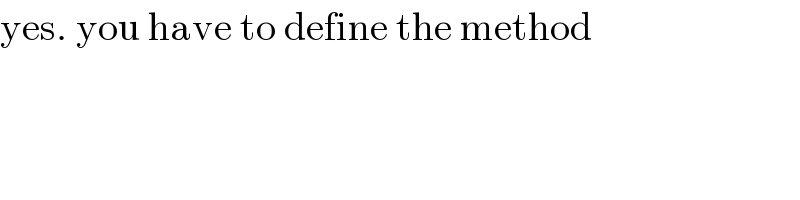
yes . you have to define the method

Commented by ajfour last updated on 17/May/19

Commented by malwaan last updated on 18/May/19

w h a t s t h e a n s w e r t o y o u r

m e t h o d s i r m r W ?

Commented by mr W last updated on 18/May/19

t h e p o s i t i o n s o f A a n d B c a n b e e x p r e s s e d

a s θ_{A} a n d θ_{B} . ∣ θ_{A} - θ_{B} ∣ i s e q u a l l y

d i s t r i b u t e d o v e r 0 ° - 180 ° . t h e p r o b a b i l i t y

f o r ∣ θ_{A} - θ_{B} ∣⩾ 120 ° i s t h e r e f o r e

\frac{180 - 120}{180} = \frac{1}{3} .

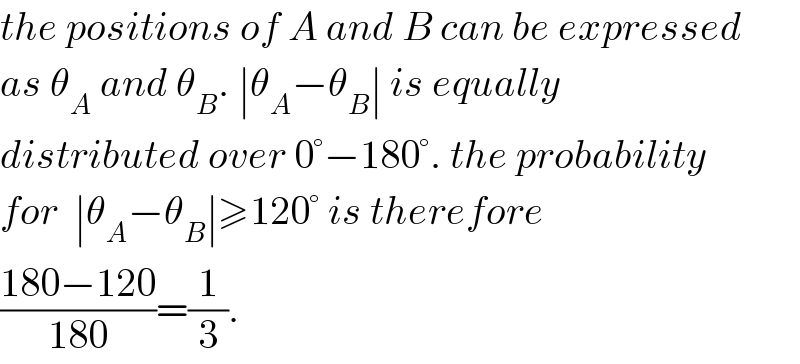
Commented by malwaan last updated on 19/May/19

t h a n k y o u s i r

Facebook Tweet Pin