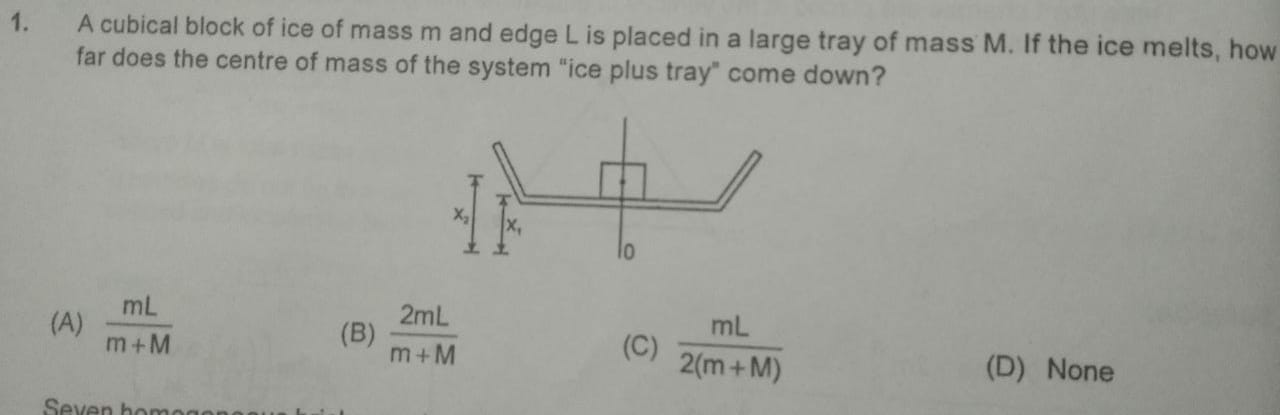
Question Number 61205 by necx1 last updated on 30/May/19
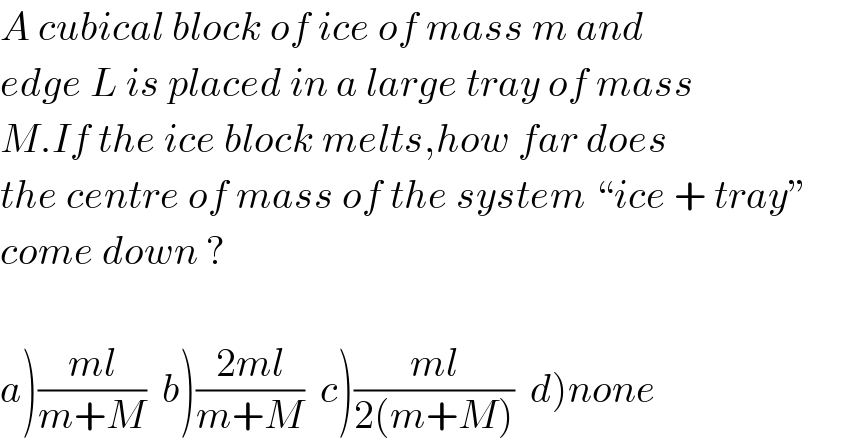
Commented by necx1 last updated on 30/May/19
Commented by mr W last updated on 30/May/19

Commented by necx1 last updated on 30/May/19
Commented by mr W last updated on 30/May/19

