Question Number 49367 by behi83417@gmail.com last updated on 06/Dec/18
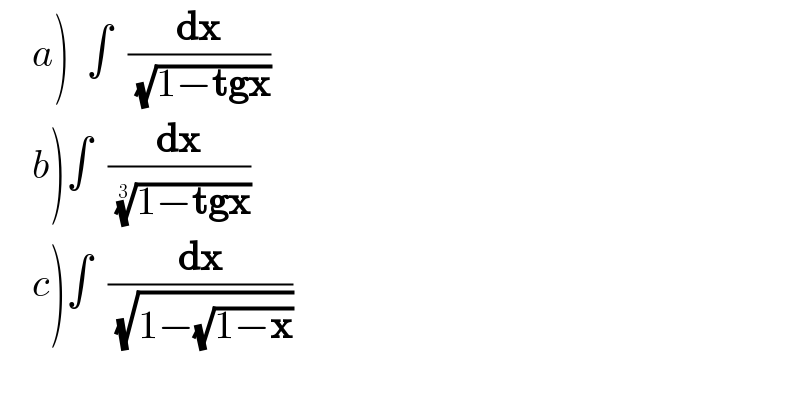
$$\left.\:\:\:\:{a}\right)\:\:\int\:\:\frac{\boldsymbol{\mathrm{dx}}}{\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{tgx}}}} \\ $$$$\left.\:\:\:\:{b}\right)\int\:\:\frac{\boldsymbol{\mathrm{dx}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{1}−\boldsymbol{\mathrm{tgx}}}} \\ $$$$\left.\:\:\:\:{c}\right)\int\:\:\frac{\boldsymbol{\mathrm{dx}}}{\:\sqrt{\mathrm{1}−\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}}}} \\ $$
Commented by behi83417@gmail.com last updated on 06/Dec/18

$${thank}\:{you}\:{very}\:{much}\:{pro}.\:{Abdo}. \\ $$
Commented by maxmathsup by imad last updated on 06/Dec/18
$${you}\:{are}\:{welcome}. \\ $$
Commented by maxmathsup by imad last updated on 06/Dec/18
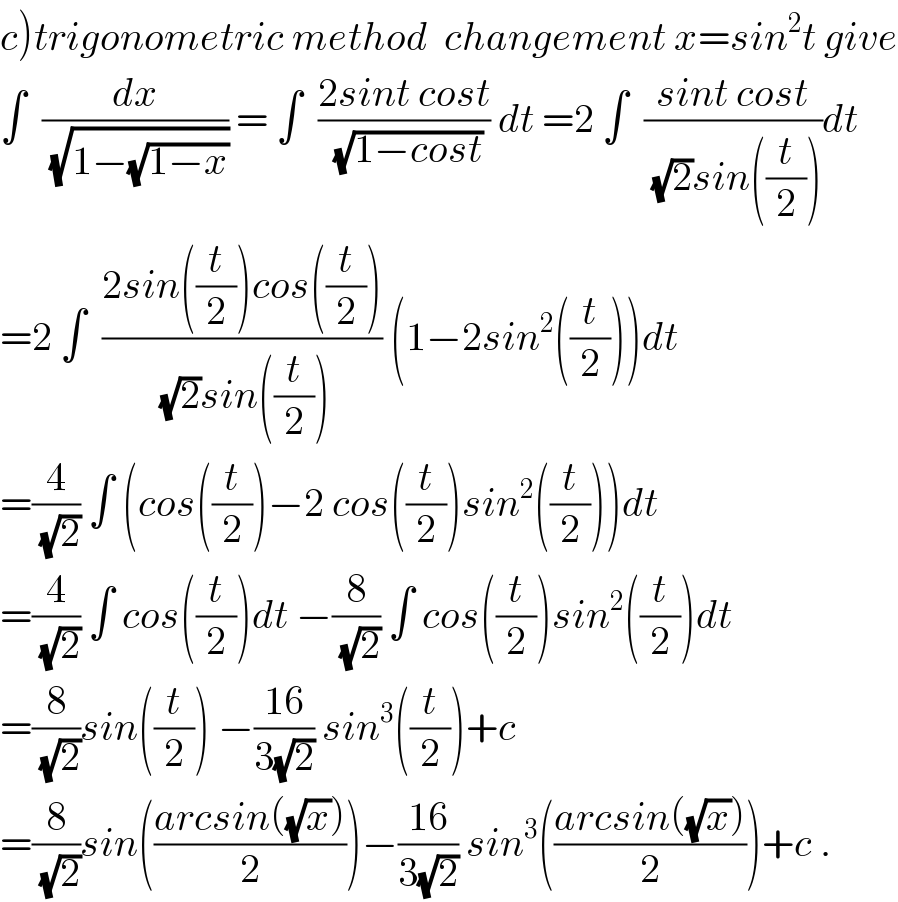
$$\left.{c}\right){trigonometric}\:{method}\:\:{changement}\:{x}={sin}^{\mathrm{2}} {t}\:{give} \\ $$$$\int\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−\sqrt{\mathrm{1}−{x}}}}\:=\:\int\:\:\frac{\mathrm{2}{sint}\:{cost}}{\:\sqrt{\mathrm{1}−{cost}}}\:{dt}\:=\mathrm{2}\:\int\:\:\frac{{sint}\:{cost}}{\:\sqrt{\mathrm{2}}{sin}\left(\frac{{t}}{\mathrm{2}}\right)}{dt} \\ $$$$=\mathrm{2}\:\int\:\:\frac{\mathrm{2}{sin}\left(\frac{{t}}{\mathrm{2}}\right){cos}\left(\frac{{t}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}{sin}\left(\frac{{t}}{\mathrm{2}}\right)}\:\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)\right){dt} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}}\:\int\:\left({cos}\left(\frac{{t}}{\mathrm{2}}\right)−\mathrm{2}\:{cos}\left(\frac{{t}}{\mathrm{2}}\right){sin}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)\right){dt} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}}\:\int\:{cos}\left(\frac{{t}}{\mathrm{2}}\right){dt}\:−\frac{\mathrm{8}}{\:\sqrt{\mathrm{2}}}\:\int\:{cos}\left(\frac{{t}}{\mathrm{2}}\right){sin}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right){dt} \\ $$$$=\frac{\mathrm{8}}{\:\sqrt{\mathrm{2}}}{sin}\left(\frac{{t}}{\mathrm{2}}\right)\:−\frac{\mathrm{16}}{\mathrm{3}\sqrt{\mathrm{2}}}\:{sin}^{\mathrm{3}} \left(\frac{{t}}{\mathrm{2}}\right)+{c} \\ $$$$=\frac{\mathrm{8}}{\:\sqrt{\mathrm{2}}}{sin}\left(\frac{{arcsin}\left(\sqrt{{x}}\right)}{\mathrm{2}}\right)−\frac{\mathrm{16}}{\mathrm{3}\sqrt{\mathrm{2}}}\:{sin}^{\mathrm{3}} \left(\frac{{arcsin}\left(\sqrt{{x}}\right)}{\mathrm{2}}\right)+{c}\:. \\ $$
Commented by maxmathsup by imad last updated on 06/Dec/18
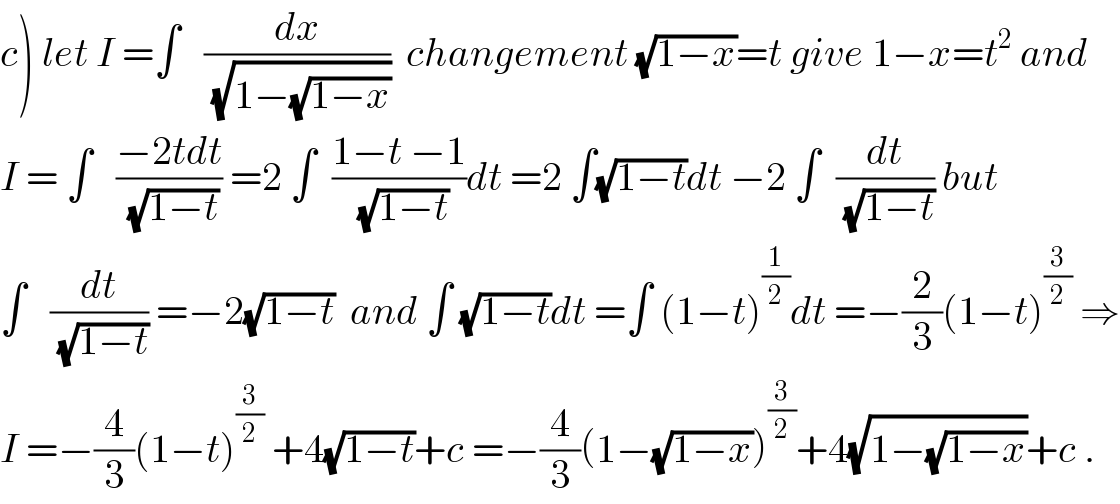
$$\left.{c}\right)\:{let}\:{I}\:=\int\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}−\sqrt{\mathrm{1}−{x}}}}\:\:{changement}\:\sqrt{\mathrm{1}−{x}}={t}\:{give}\:\mathrm{1}−{x}={t}^{\mathrm{2}} \:{and} \\ $$$${I}\:=\:\int\:\:\:\frac{−\mathrm{2}{tdt}}{\:\sqrt{\mathrm{1}−{t}}}\:=\mathrm{2}\:\int\:\:\frac{\mathrm{1}−{t}\:−\mathrm{1}}{\:\sqrt{\mathrm{1}−{t}}}{dt}\:=\mathrm{2}\:\int\sqrt{\mathrm{1}−{t}}{dt}\:−\mathrm{2}\:\int\:\:\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}}}\:{but} \\ $$$$\int\:\:\:\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}}}\:=−\mathrm{2}\sqrt{\mathrm{1}−{t}}\:\:{and}\:\int\:\sqrt{\mathrm{1}−{t}}{dt}\:=\int\:\left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt}\:=−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{1}−{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:+\mathrm{4}\sqrt{\mathrm{1}−{t}}+{c}\:=−\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{4}\sqrt{\mathrm{1}−\sqrt{\mathrm{1}−{x}}}+{c}\:. \\ $$
Commented by behi83417@gmail.com last updated on 06/Dec/18
$${nice}\:{method}.{i}\:{love}\:{this}.{thanks}\:{a}\:{lot}. \\ $$
Answered by MJS last updated on 06/Dec/18
![(a) ∫(dx/( (√(1−tan x))))= [t=(√(1−tan x)) → dx=−((2tdt)/(t^4 −2t^2 +2))] =−2∫(dt/(t^4 −2t^2 +2))=−2∫(dt/((t^2 −(√(2+2(√2)))t+(√2))(t^2 +(√(2+2(√2)))t+(√2))))= =−2∫(dt/((t^2 −pt+q)(t^2 +pt+q)))= =(1/(pq))∫((t−p)/(t^2 −pt+q))dt−(1/(pq))∫((t+p)/(t^2 +pt+q))dt and these can be solved](https://www.tinkutara.com/question/Q49377.png)
$$\left({a}\right) \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{1}−\mathrm{tan}\:{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{1}−\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=−\frac{\mathrm{2}{tdt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}}\right] \\ $$$$=−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}}=−\mathrm{2}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{t}+\sqrt{\mathrm{2}}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{t}+\sqrt{\mathrm{2}}\right)}= \\ $$$$=−\mathrm{2}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −{pt}+{q}\right)\left({t}^{\mathrm{2}} +{pt}+{q}\right)}= \\ $$$$=\frac{\mathrm{1}}{{pq}}\int\frac{{t}−{p}}{{t}^{\mathrm{2}} −{pt}+{q}}{dt}−\frac{\mathrm{1}}{{pq}}\int\frac{{t}+{p}}{{t}^{\mathrm{2}} +{pt}+{q}}{dt} \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Dec/18
![a)∫(dx/( (√(1−tanx)))) t^2 =1−tanx 2tdt=−sec^2 xdx dx=((−2tdt)/(1+(1−t^2 )^2 )) ∫((−2tdt)/(t×{1+(1−t^2 )^2 })) =−2∫(dt/(t^4 −2t^2 +2)) =−2∫((1/t^2 )/(t^2 −2+(2/t^2 )))dt now t^2 +(2/t^2 )=(t+((√2)/t))^2 −2(√2) =(t−((√2)/t))^2 +2(√2) d(t+((√2)/t))=(1−((√2)/t^2 ))dt d(t−((√2)/t))=(1+((√2)/t^2 ))dt =((−1)/( (√2)))∫(((2(√2))/t^2 )/(t^2 −2+(2/t^2 )))dt =((−1)/( (√2)))∫(((1+((√2)/t^2 ))−(1−((√2)/t^2 )))/(t^2 −2+(2/t^2 )))dt =((−1)/( (√2)))[∫((1+((√2)/t^2 ))/((t−((√2)/t))^2 +2(√2)))dt−∫((1−((√2)/t^2 ))/((t+((√2)/t))^2 −2(√2)))dt] =((−1)/( (√2)))[(1/( (√(2(√2) ))))tan^(−1) (((t−((√2)/t))/( (√(2(√2))))))−(1/(2(√(2(√2)))))ln{(((t+((√2)/t))−(√(2(√2))))/((t+((√2)/t))+(√(2(√2)))))}+c now pls put t=(√(1−tanx))](https://www.tinkutara.com/question/Q49378.png)
$$\left.{a}\right)\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{tanx}}}\:\:\: \\ $$$${t}^{\mathrm{2}} =\mathrm{1}−{tanx}\:\:\mathrm{2}{tdt}=−{sec}^{\mathrm{2}} {xdx} \\ $$$${dx}=\frac{−\mathrm{2}{tdt}}{\mathrm{1}+\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\int\frac{−\mathrm{2}{tdt}}{{t}×\left\{\mathrm{1}+\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} \right\}} \\ $$$$=−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}} \\ $$$$=−\mathrm{2}\int\frac{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{2}}{{t}^{\mathrm{2}} }}{dt} \\ $$$${now}\:{t}^{\mathrm{2}} +\frac{\mathrm{2}}{{t}^{\mathrm{2}} }=\left({t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({t}−\frac{\sqrt{\mathrm{2}}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}\: \\ $$$${d}\left({t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)=\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }\right){dt} \\ $$$${d}\left({t}−\frac{\sqrt{\mathrm{2}}}{{t}}\right)=\left(\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }\right){dt} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\frac{\mathrm{2}\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{2}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\left(\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }\right)}{{t}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{2}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\int\frac{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }}{\left({t}−\frac{\sqrt{\mathrm{2}}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}}{dt}−\int\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} }}{\left({t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}}{dt}\right] \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}\:}}{tan}^{−\mathrm{1}} \left(\frac{{t}−\frac{\sqrt{\mathrm{2}}}{{t}}}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}}{ln}\left\{\frac{\left({t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)−\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}}{\left({t}+\frac{\sqrt{\mathrm{2}}}{{t}}\right)+\sqrt{\mathrm{2}\sqrt{\mathrm{2}}}}\right\}+{c}\right. \\ $$$${now}\:{pls}\:{put}\:{t}=\sqrt{\mathrm{1}−{tanx}}\: \\ $$$$ \\ $$
Commented by behi83417@gmail.com last updated on 06/Dec/18
$${thanks}\:{in}\:{advance}\:{sir}\:{MJS}\:{and}\:{sir}\:{tanmay}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Dec/18
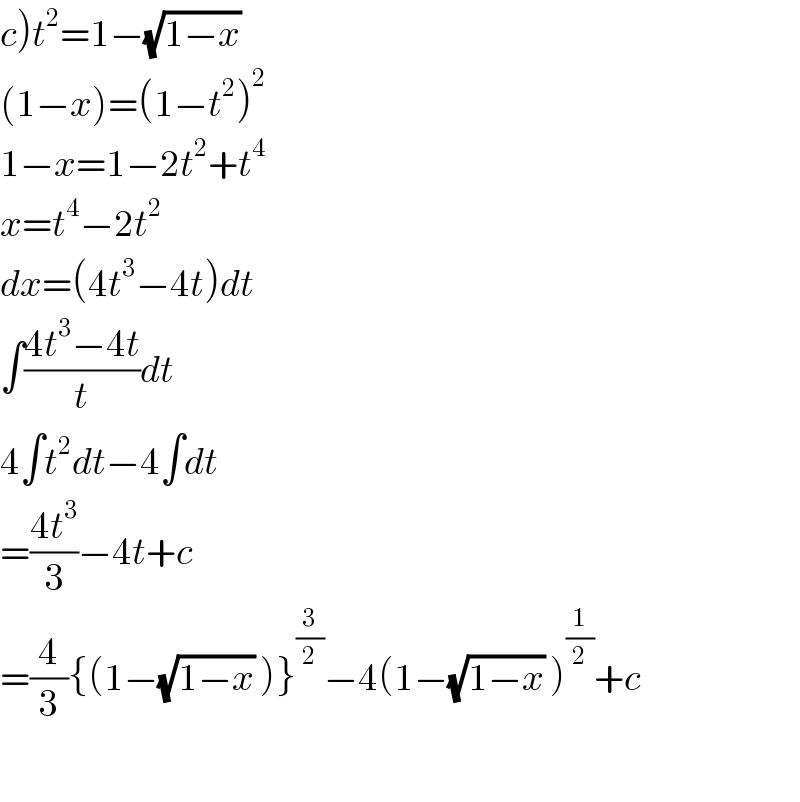
$$\left.{c}\right){t}^{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{1}−{x}}\: \\ $$$$\left(\mathrm{1}−{x}\right)=\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{1}−{x}=\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \\ $$$${x}={t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:\: \\ $$$${dx}=\left(\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}\right){dt} \\ $$$$\int\frac{\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}}{{t}}{dt} \\ $$$$\mathrm{4}\int{t}^{\mathrm{2}} {dt}−\mathrm{4}\int{dt} \\ $$$$=\frac{\mathrm{4}{t}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{4}{t}+{c} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\left\{\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}}\:\right)\right\}^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{4}\left(\mathrm{1}−\sqrt{\mathrm{1}−{x}}\:\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +{c} \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Dec/18
$${trying}\:{to}\:{solve}\:{q}.{no}\:\left({b}\right)…{excellent}\:{posts}\:{from}\:{your}\:{side}\:{sir}.. \\ $$
Commented by behi83417@gmail.com last updated on 06/Dec/18
$${thank}\:{you}\:{so}\:{much}\:{sir}. \\ $$
Commented by behi83417@gmail.com last updated on 06/Dec/18
$${you}\:{are}\:{wellcome}\:{sir}.{one}\:{of}\:\:{the}\:{best}\: \\ $$$${question}\:{solvers}\:{with}\:{great}\:{works} \\ $$$${in}\:{this}\:{lovely}\:{forum}\:{is}:{sir}\:{tanmay}. \\ $$$${godlock}\:{dear}. \\ $$
Answered by MJS last updated on 06/Dec/18
![(b) ∫(dx/((1−tan x)^(1/3) ))= [t=(1−tan x)^(1/3) → dx=−((3t^2 )/(t^6 −2t^3 +2))] =−3∫(t/(t^6 −2t^3 +2))dt t^6 −2t^3 +2=(t^2 +(4)^(1/3) t+(2)^(1/3) )(t^2 −((1−(√3))/( (2)^(1/3) ))t+(2)^(1/3) )(t^2 −((1+(√3))/( (2)^(1/3) ))t+(2)^(1/3) )= =(t^2 +pt+q)(t^2 +rt+q)(t^2 +st+q) ⇒ ⇒ (3/(q(p−r)(p−s)))∫((t+p)/(t^2 +pt+q))dt+(3/(q(r−p)(r−s)))∫((t+r)/(t^2 +rt+q))dt+(3/(q(s−p)(s−r)))∫((t+s)/(t^2 +st+q))dt ...and again we can solve these](https://www.tinkutara.com/question/Q49411.png)
$$\left({b}\right) \\ $$$$\int\frac{{dx}}{\left(\mathrm{1}−\mathrm{tan}\:{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }= \\ $$$$\:\:\:\:\:\left[{t}=\left(\mathrm{1}−\mathrm{tan}\:{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\rightarrow\:{dx}=−\frac{\mathrm{3}{t}^{\mathrm{2}} }{{t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}}\right] \\ $$$$=−\mathrm{3}\int\frac{{t}}{{t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}}{dt} \\ $$$${t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}=\left({t}^{\mathrm{2}} +\sqrt[{\mathrm{3}}]{\mathrm{4}}{t}+\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)\left({t}^{\mathrm{2}} −\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}}{t}+\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)\left({t}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}}{t}+\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)= \\ $$$$=\left({t}^{\mathrm{2}} +{pt}+{q}\right)\left({t}^{\mathrm{2}} +{rt}+{q}\right)\left({t}^{\mathrm{2}} +{st}+{q}\right)\:\Rightarrow \\ $$$$\Rightarrow\:\frac{\mathrm{3}}{{q}\left({p}−{r}\right)\left({p}−{s}\right)}\int\frac{{t}+{p}}{{t}^{\mathrm{2}} +{pt}+{q}}{dt}+\frac{\mathrm{3}}{{q}\left({r}−{p}\right)\left({r}−{s}\right)}\int\frac{{t}+{r}}{{t}^{\mathrm{2}} +{rt}+{q}}{dt}+\frac{\mathrm{3}}{{q}\left({s}−{p}\right)\left({s}−{r}\right)}\int\frac{{t}+{s}}{{t}^{\mathrm{2}} +{st}+{q}}{dt} \\ $$$$…\mathrm{and}\:\mathrm{again}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{these} \\ $$
Commented by behi83417@gmail.com last updated on 06/Dec/18
$${ok}!\:{thanks}.\:{waiting}….. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Dec/18
![b)t^3 =1−tanx 3t^2 dt=−sec^2 xdx dx=((−3t^2 )/(1+(1−t^3 )^2 ))dt=((−3t^2 )/(t^6 −2t^3 +2))dt ∫((−3t^2 )/(t^6 −2t^3 +2))×(1/t)dt =−3∫((tdt)/(t^6 −2t^3 +2)) t^6 −2t^3 +2 =(t^3 )^2 −2×t^3 ×1+1+1 =−3∫((tdt)/((t^3 −1)^2 −i^2 )) =−3∫((tdt)/((t^3 −1−i)(t^3 −1+i))) =−3∫((tdt)/((t^3 +a)(t^3 +b))) [a=−1−i b=−1+i] =((−3)/(a−b))∫[((t(t^3 +a)−t(t^3 +b))/((t^3 +a)(t^3 +b)))]dt =(3/(b−a))[∫((tdt)/(t^3 +b))−∫((tdt)/(t^3 +a))] now solving ∫((tdt)/(t^3 +a)) ∫((tdt)/((t+^3 (√a) )(t^2 −t×^3 (√a) +^(2/3) (√a) ))) ∫((tdt)/((t+p)(t^2 −tp+p^2 ))) (t/((t+p)(t^2 −tp+p^2 )))=(A/(t+p))+((Bt+C)/(t^2 −tp+p^2 )) t=A(t^2 −tp+p^2 )+(Bt+C)(t+p) t=t^2 (A+B)+t(−Ap+Bp+C)+Ap^2 +Cp A+B=0 Ap^2 +Cp=0 −Ap+Bp+C=1 C=−Ap −Ap−Ap−Ap=1 A=((−1)/(3p)) B=(1/(3p)) C=((−1)/3) ∫(A/(t+p))dt+∫((Bt+C)/(t^2 −tp+p^2 ))dt ((−1)/(3p))∫(dt/(t+p))+∫(((1/(3p))t+((−1)/3))/(t^2 −tp+p^2 ))dt ((−1)/(3p))∫(dt/(t+p))+(1/3)∫((t−1)/(t^2 −tp+p^2 ))dt ((−1)/(3p))∫(dt/(t+p))+(1/6)∫((2t−p+p−2)/(t^2 −tp+p^2 )) ((−1)/(3p))∫(dt/(t+p))+(1/6)∫((d(t^2 −tp+p^2 ))/(t^2 −tp+p^2 ))+((p−2)/6)∫(dt/(t^2 −2.t.(p/2)+(p^2 /4)+((3p^2 )/4))) ((−1)/(3p))ln(t+p)+(1/6)ln(t^2 −tp+p^2 )+((p−2)/6)×(1/(((((√3) p)/2))^ ))×tan^(−1) (((t−(p/2))/(((√3) p)/2)))+c_1 now put p=(a)^(1/3) next put a=(−1−i) similarly we can find ∫((tdt)/(t^3 +b)) in place of p put (b)^(1/3) next put b=(−1+i) finaly algebric addition...](https://www.tinkutara.com/question/Q49458.png)
$$\left.{b}\right){t}^{\mathrm{3}} =\mathrm{1}−{tanx}\: \\ $$$$\mathrm{3}{t}^{\mathrm{2}} {dt}=−{sec}^{\mathrm{2}} {xdx} \\ $$$${dx}=\frac{−\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{1}+\left(\mathrm{1}−{t}^{\mathrm{3}} \right)^{\mathrm{2}} }{dt}=\frac{−\mathrm{3}{t}^{\mathrm{2}} }{{t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}}{dt} \\ $$$$\int\frac{−\mathrm{3}{t}^{\mathrm{2}} }{{t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}}×\frac{\mathrm{1}}{{t}}{dt} \\ $$$$=−\mathrm{3}\int\frac{{tdt}}{{t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}} \\ $$$${t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2} \\ $$$$=\left({t}^{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{2}×{t}^{\mathrm{3}} ×\mathrm{1}+\mathrm{1}+\mathrm{1} \\ $$$$=−\mathrm{3}\int\frac{{tdt}}{\left({t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} −{i}^{\mathrm{2}} } \\ $$$$=−\mathrm{3}\int\frac{{tdt}}{\left({t}^{\mathrm{3}} −\mathrm{1}−{i}\right)\left({t}^{\mathrm{3}} −\mathrm{1}+{i}\right)} \\ $$$$=−\mathrm{3}\int\frac{{tdt}}{\left({t}^{\mathrm{3}} +{a}\right)\left({t}^{\mathrm{3}} +{b}\right)}\:\left[{a}=−\mathrm{1}−{i}\:\:\:\:{b}=−\mathrm{1}+{i}\right] \\ $$$$=\frac{−\mathrm{3}}{{a}−{b}}\int\left[\frac{{t}\left({t}^{\mathrm{3}} +{a}\right)−{t}\left({t}^{\mathrm{3}} +{b}\right)}{\left({t}^{\mathrm{3}} +{a}\right)\left({t}^{\mathrm{3}} +{b}\right)}\right]{dt} \\ $$$$=\frac{\mathrm{3}}{{b}−{a}}\left[\int\frac{{tdt}}{{t}^{\mathrm{3}} +{b}}−\int\frac{{tdt}}{{t}^{\mathrm{3}} +{a}}\right] \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{solving}}\:\int\frac{{tdt}}{{t}^{\mathrm{3}} +{a}} \\ $$$$\int\frac{{tdt}}{\left({t}+^{\mathrm{3}} \sqrt{{a}}\:\right)\left({t}^{\mathrm{2}} −{t}×^{\mathrm{3}} \sqrt{{a}}\:+^{\frac{\mathrm{2}}{\mathrm{3}}} \sqrt{{a}}\:\right)} \\ $$$$\int\frac{{tdt}}{\left({t}+{p}\right)\left({t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} \right)} \\ $$$$\frac{{t}}{\left({t}+{p}\right)\left({t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} \right)}=\frac{{A}}{{t}+{p}}+\frac{{Bt}+{C}}{{t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} } \\ $$$${t}={A}\left({t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} \right)+\left({Bt}+{C}\right)\left({t}+{p}\right) \\ $$$${t}={t}^{\mathrm{2}} \left({A}+{B}\right)+{t}\left(−{Ap}+{Bp}+{C}\right)+{Ap}^{\mathrm{2}} +{Cp} \\ $$$${A}+{B}=\mathrm{0} \\ $$$${Ap}^{\mathrm{2}} +{Cp}=\mathrm{0} \\ $$$$−{Ap}+{Bp}+{C}=\mathrm{1} \\ $$$${C}=−{Ap} \\ $$$$−{Ap}−{Ap}−{Ap}=\mathrm{1}\:\:\:\:{A}=\frac{−\mathrm{1}}{\mathrm{3}{p}}\:\:\:{B}=\frac{\mathrm{1}}{\mathrm{3}{p}}\:\:\:\:{C}=\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$$\int\frac{{A}}{{t}+{p}}{dt}+\int\frac{{Bt}+{C}}{{t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} }{dt} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}{p}}\int\frac{{dt}}{{t}+{p}}+\int\frac{\frac{\mathrm{1}}{\mathrm{3}{p}}{t}+\frac{−\mathrm{1}}{\mathrm{3}}}{{t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} }{dt} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}{p}}\int\frac{{dt}}{{t}+{p}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} }{dt} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}{p}}\int\frac{{dt}}{{t}+{p}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{t}−{p}+{p}−\mathrm{2}}{{t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} } \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}{p}}\int\frac{{dt}}{{t}+{p}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{d}\left({t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} }+\frac{{p}−\mathrm{2}}{\mathrm{6}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}.{t}.\frac{{p}}{\mathrm{2}}+\frac{{p}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{3}{p}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}{p}}{ln}\left({t}+{p}\right)+\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({t}^{\mathrm{2}} −{tp}+{p}^{\mathrm{2}} \right)+\frac{{p}−\mathrm{2}}{\mathrm{6}}×\frac{\mathrm{1}}{\left(\frac{\sqrt{\mathrm{3}}\:{p}}{\mathrm{2}}\right)^{} }×{tan}^{−\mathrm{1}} \left(\frac{{t}−\frac{{p}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}\:{p}}{\mathrm{2}}}\right)+{c}_{\mathrm{1}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{put}}\:\boldsymbol{{p}}=\left(\boldsymbol{{a}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \: \\ $$$$\boldsymbol{{next}}\:\boldsymbol{{put}}\:\boldsymbol{{a}}=\left(−\mathrm{1}−\boldsymbol{{i}}\right) \\ $$$$\boldsymbol{{similarly}}\:\boldsymbol{{we}}\:\boldsymbol{{can}}\:\boldsymbol{{find}}\:\int\frac{{tdt}}{{t}^{\mathrm{3}} +{b}} \\ $$$${in}\:{place}\:{of}\:{p}\:{put}\:\left({b}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${next}\:{put}\:{b}=\left(−\mathrm{1}+{i}\right) \\ $$$${finaly}\:{algebric}\:{addition}… \\ $$$$ \\ $$
Commented by behi83417@gmail.com last updated on 07/Dec/18
$${great}\:{work}\:{done}\:{by}\:{you}.{thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Dec/18

$${thank}\:{you}\:{sir}… \\ $$
