Question Number 157753 by Engr_Jidda last updated on 27/Oct/21

$${A}\:{farmer}\:{has}\:{numbers}\:{of}\:{animals} \\ $$$${in}\:{his}\:{farm}\:{made}\:{up}\:{of}\:{hens}\:{and}\:{goats}. \\ $$$${One}\:{morning}\:{he}\:{counted}\:\mathrm{20}\:{heads}\:{and}\:\mathrm{66}\:{legs} \\ $$$${of}\:{the}\:{animals}.\:{How}\:{many}\:{hens}\:{and} \\ $$$${goat}\:{were}\:{counted}\:{by}\:{the}\:{farmer}. \\ $$
Answered by Kunal12588 last updated on 27/Oct/21
![let number of hens be x and number of goats be y Total number of heads = 20 ⇒x+y=20 ....[1] Total number of legs = 66 ⇒2x+4y=66 ⇒x+2y=33 ...[2] subtracting [1] from [2] y=13 putting value if y in equation [1] x=7 Therefore there were 7 hens and 13 goats](https://www.tinkutara.com/question/Q157760.png)
$$\mathrm{let}\:\mathrm{number}\:\mathrm{of}\:\mathrm{hens}\:\mathrm{be}\:{x} \\ $$$$\mathrm{and}\:\mathrm{number}\:\mathrm{of}\:\mathrm{goats}\:\mathrm{be}\:{y} \\ $$$$\mathrm{Total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{heads}\:=\:\mathrm{20} \\ $$$$\Rightarrow{x}+{y}=\mathrm{20}\:….\left[\mathrm{1}\right] \\ $$$$\mathrm{Total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{legs}\:=\:\mathrm{66} \\ $$$$\Rightarrow\mathrm{2}{x}+\mathrm{4}{y}=\mathrm{66} \\ $$$$\Rightarrow{x}+\mathrm{2}{y}=\mathrm{33}\:…\left[\mathrm{2}\right] \\ $$$$\mathrm{subtracting}\:\left[\mathrm{1}\right]\:\mathrm{from}\:\left[\mathrm{2}\right] \\ $$$${y}=\mathrm{13} \\ $$$$\mathrm{putting}\:\mathrm{value}\:\mathrm{if}\:{y}\:\mathrm{in}\:\mathrm{equation}\:\left[\mathrm{1}\right] \\ $$$${x}=\mathrm{7} \\ $$$$\mathrm{Therefore}\:\mathrm{there}\:\mathrm{were}\:\mathrm{7}\:\mathrm{hens}\:\mathrm{and}\:\mathrm{13}\:\mathrm{goats} \\ $$
Answered by som(math1967) last updated on 27/Oct/21
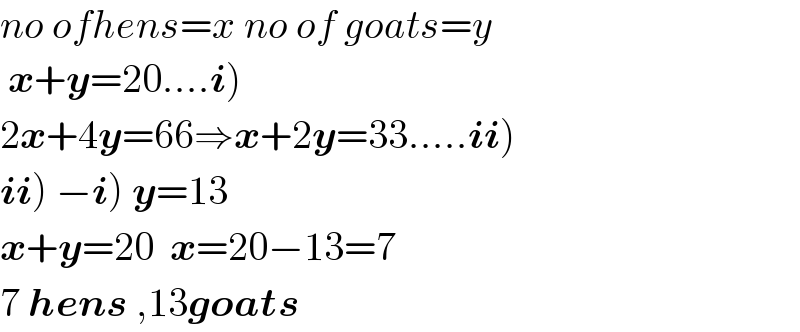
$${no}\:{ofhens}={x}\:{no}\:{of}\:{goats}={y} \\ $$$$\left.\:\boldsymbol{{x}}+\boldsymbol{{y}}=\mathrm{20}….\boldsymbol{{i}}\right) \\ $$$$\left.\mathrm{2}\boldsymbol{{x}}+\mathrm{4}\boldsymbol{{y}}=\mathrm{66}\Rightarrow\boldsymbol{{x}}+\mathrm{2}\boldsymbol{{y}}=\mathrm{33}…..\boldsymbol{{ii}}\right) \\ $$$$\left.\boldsymbol{{i}}\left.\boldsymbol{{i}}\right)\:−\boldsymbol{{i}}\right)\:\boldsymbol{{y}}=\mathrm{13} \\ $$$$\boldsymbol{{x}}+\boldsymbol{{y}}=\mathrm{20}\:\:\boldsymbol{{x}}=\mathrm{20}−\mathrm{13}=\mathrm{7} \\ $$$$\mathrm{7}\:\boldsymbol{{hens}}\:,\mathrm{13}\boldsymbol{{goats}} \\ $$
Commented by Engr_Jidda last updated on 27/Oct/21

$${thanks} \\ $$
Answered by mr W last updated on 27/Oct/21

$${we}\:{have}\:\mathrm{20}\:{animals}\:{and}\:\mathrm{66}\:{legs}. \\ $$$${now}\:{each}\:{animal}\:{should}\:{hide}\:{two}\:{legs}, \\ $$$${then}\:\mathrm{66}−\mathrm{20}×\mathrm{2}=\mathrm{26}\:{legs}\:{remain}.\:{these} \\ $$$${legs}\:{are}\:{the}\:{remaining}\:{legs}\:{from}\: \\ $$$${the}\:{goats},\:{because}\:{all}\:{legs}\:{from}\:{the} \\ $$$${hens}\:{are}\:{hidden}.\:{since}\:{each}\:{goat}\:{has}\: \\ $$$$\mathrm{2}\:{legs}\:{remaining},\:{so}\:{the}\:{number}\:{of} \\ $$$${goats}\:{is}\:\mathrm{26}/\mathrm{2}=\mathrm{13}.\:{then}\:{the}\:{number}\: \\ $$$${of}\:{hens}\:{is}\:\mathrm{20}−\mathrm{13}=\mathrm{7}. \\ $$
Commented by Engr_Jidda last updated on 27/Oct/21

$${thanks} \\ $$
