Question Number 22059 by tawa tawa last updated on 10/Oct/17

$$\mathrm{A}\:\mathrm{flywheel}\:\mathrm{whose}\:\mathrm{diameter}\:\mathrm{is}\:\mathrm{1}.\mathrm{5m}\:\mathrm{decrease}\:\mathrm{uniformly}\:\mathrm{from}\:\mathrm{240rad}/\mathrm{min} \\ $$$$\mathrm{until}\:\mathrm{it}\:\mathrm{came}\:\mathrm{to}\:\mathrm{rest}\:\mathrm{10s}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{revolution}\:\mathrm{made}. \\ $$
Answered by Tinkutara last updated on 10/Oct/17
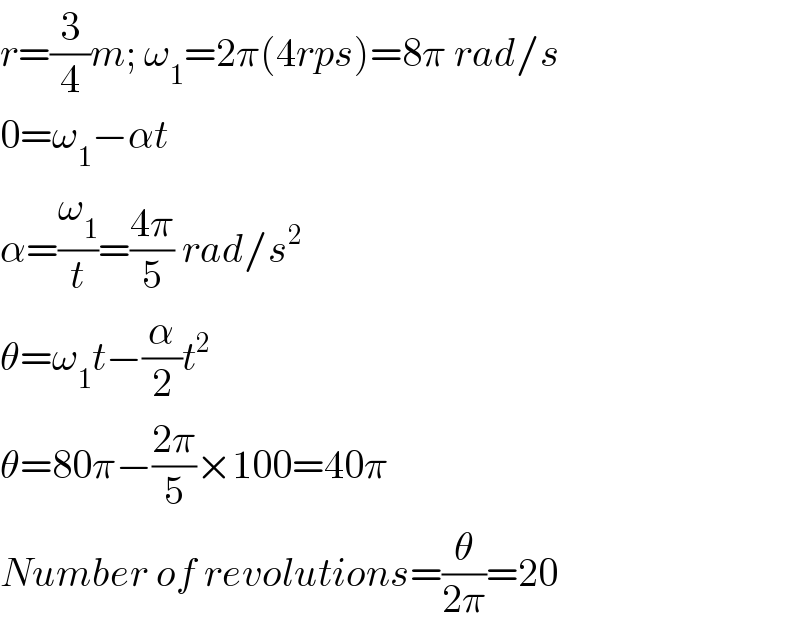
$${r}=\frac{\mathrm{3}}{\mathrm{4}}{m};\:\omega_{\mathrm{1}} =\mathrm{2}\pi\left(\mathrm{4}{rps}\right)=\mathrm{8}\pi\:{rad}/{s} \\ $$$$\mathrm{0}=\omega_{\mathrm{1}} −\alpha{t} \\ $$$$\alpha=\frac{\omega_{\mathrm{1}} }{{t}}=\frac{\mathrm{4}\pi}{\mathrm{5}}\:{rad}/{s}^{\mathrm{2}} \\ $$$$\theta=\omega_{\mathrm{1}} {t}−\frac{\alpha}{\mathrm{2}}{t}^{\mathrm{2}} \\ $$$$\theta=\mathrm{80}\pi−\frac{\mathrm{2}\pi}{\mathrm{5}}×\mathrm{100}=\mathrm{40}\pi \\ $$$${Number}\:{of}\:{revolutions}=\frac{\theta}{\mathrm{2}\pi}=\mathrm{20} \\ $$
Commented by tawa tawa last updated on 10/Oct/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
