Question Number 40498 by Necxx last updated on 23/Jul/18

$${A}\:{gas}\:{at}\:\mathrm{17}°\:{has}\:{the}\:{ratio}\:{of}\:{its}\:{initial} \\ $$$${to}\:{final}\:{volume}\:{as}\:\mathrm{25}\:{with}\:{initial} \\ $$$${pressure}\:{of}\:\mathrm{2}×\mathrm{10}^{\mathrm{5}} {Nm}^{−\mathrm{2}} .{Calculate} \\ $$$${the}\:{final}\:{pressure}\:{and}\:{temperature} \\ $$$${after}\:{compression}.\left(\gamma=\mathrm{1}.\mathrm{5}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18
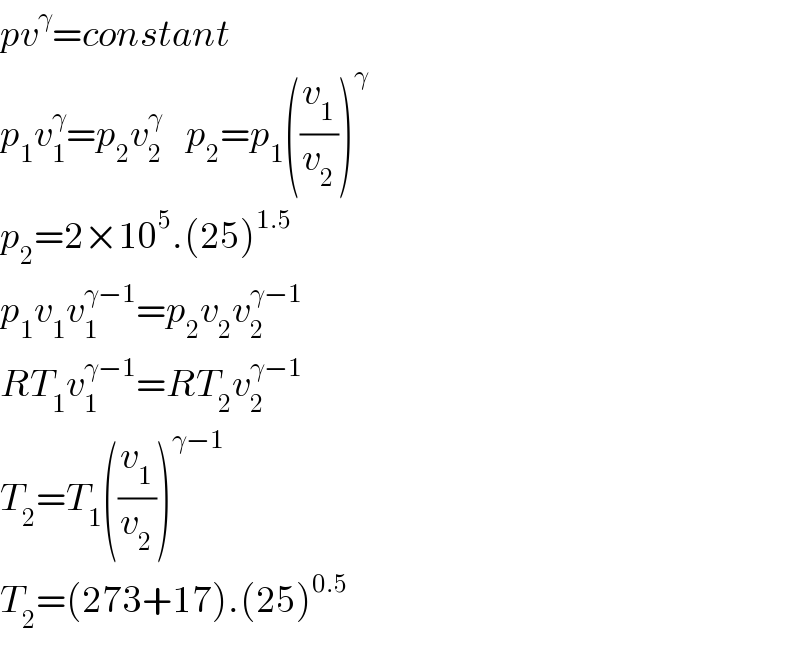
$${pv}^{\gamma} ={constant} \\ $$$${p}_{\mathrm{1}} {v}_{\mathrm{1}} ^{\gamma} ={p}_{\mathrm{2}} {v}_{\mathrm{2}} ^{\gamma} \:\:\:\:{p}_{\mathrm{2}} ={p}_{\mathrm{1}} \left(\frac{{v}_{\mathrm{1}} }{{v}_{\mathrm{2}} }\right)^{\gamma} \:\: \\ $$$${p}_{\mathrm{2}} =\mathrm{2}×\mathrm{10}^{\mathrm{5}} .\left(\mathrm{25}\right)^{\mathrm{1}.\mathrm{5}} \\ $$$${p}_{\mathrm{1}} {v}_{\mathrm{1}} {v}_{\mathrm{1}} ^{\gamma−\mathrm{1}} ={p}_{\mathrm{2}} {v}_{\mathrm{2}} {v}_{\mathrm{2}} ^{\gamma−\mathrm{1}} \: \\ $$$${RT}_{\mathrm{1}} {v}_{\mathrm{1}} ^{\gamma−\mathrm{1}} ={RT}_{\mathrm{2}} {v}_{\mathrm{2}} ^{\gamma−\mathrm{1}} \\ $$$${T}_{\mathrm{2}} ={T}_{\mathrm{1}} \left(\frac{{v}_{\mathrm{1}} }{{v}_{\mathrm{2}} }\right)^{\gamma−\mathrm{1}} \\ $$$${T}_{\mathrm{2}} =\left(\mathrm{273}+\mathrm{17}\right).\left(\mathrm{25}\right)^{\mathrm{0}.\mathrm{5}} \\ $$
