Question Number 104301 by aurpeyz last updated on 20/Jul/20

$$\mathrm{a}\:\mathrm{girl}\:\mathrm{weighs}\:\mathrm{569}.\mathrm{37N}\:\mathrm{on}\:\mathrm{the}\:\mathrm{earth}\:\mathrm{surfsce}\:\left(\mathrm{a}\right)\:\mathrm{what}\:\mathrm{would}\:\mathrm{she}\:\mathrm{weigh}\:\mathrm{at}\:\mathrm{a}\:\mathrm{height}\:\mathrm{above}\:\mathrm{the}\:\mathrm{earth}\:\mathrm{surface}\:\mathrm{of}\:\mathrm{one}\:\mathrm{earth}\:\mathrm{radius}?\:\mathrm{what}\:\mathrm{would}\:\mathrm{her}\:\mathrm{mass}\:\mathrm{be}? \\ $$
Commented by mr W last updated on 20/Jul/20
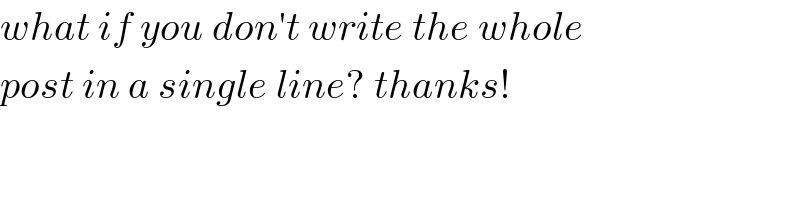
$${what}\:{if}\:{you}\:{don}'{t}\:{write}\:{the}\:{whole} \\ $$$${post}\:{in}\:{a}\:{single}\:{line}?\:{thanks}! \\ $$
Commented by aurpeyz last updated on 01/Aug/20
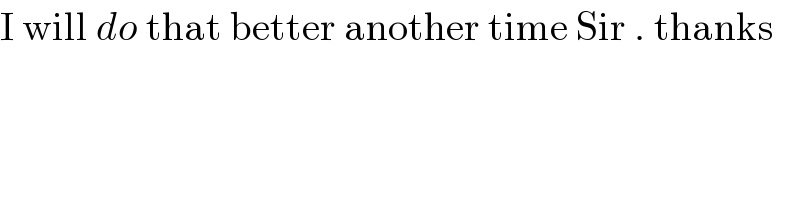
$$\mathrm{I}\:\mathrm{will}\:{do}\:\mathrm{that}\:\mathrm{better}\:\mathrm{another}\:\mathrm{time}\:\mathrm{Sir}\:.\:\mathrm{thanks} \\ $$
Answered by OlafThorendsen last updated on 20/Jul/20
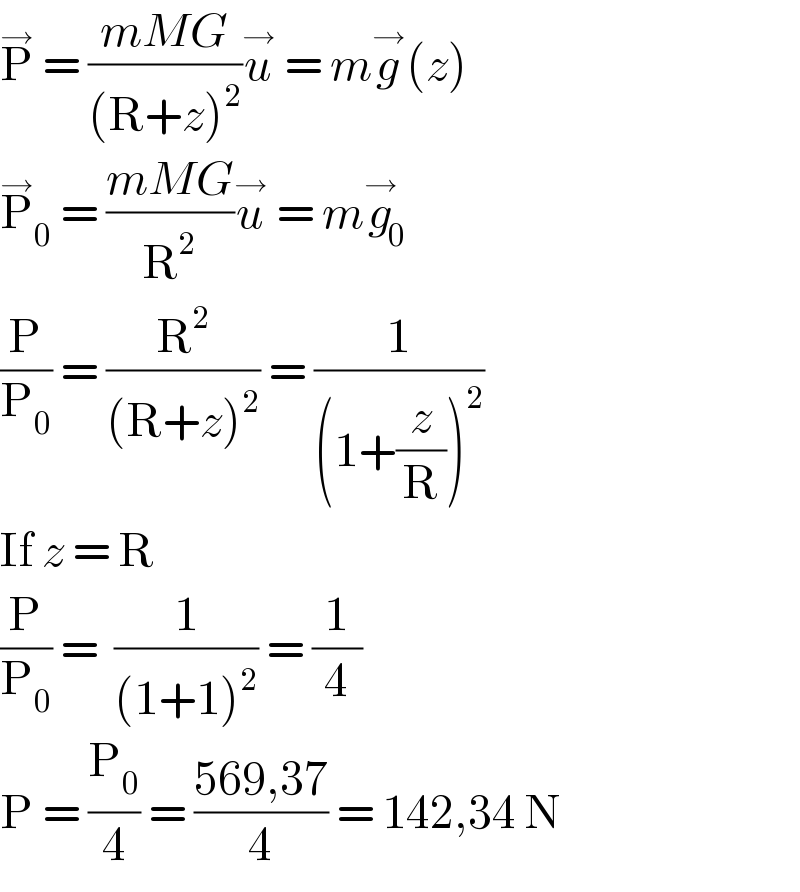
$$\overset{\rightarrow} {\mathrm{P}}\:=\:\frac{{mMG}}{\left(\mathrm{R}+{z}\right)^{\mathrm{2}} }\overset{\rightarrow} {{u}}\:=\:{m}\overset{\rightarrow} {{g}}\left({z}\right) \\ $$$$\overset{\rightarrow} {\mathrm{P}}_{\mathrm{0}} \:=\:\frac{{mMG}}{\mathrm{R}^{\mathrm{2}} }\overset{\rightarrow} {{u}}\:=\:{m}\overset{\rightarrow} {{g}}_{\mathrm{0}} \\ $$$$\frac{\mathrm{P}}{\mathrm{P}_{\mathrm{0}} }\:=\:\frac{\mathrm{R}^{\mathrm{2}} }{\left(\mathrm{R}+{z}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{{z}}{\mathrm{R}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{If}\:{z}\:=\:\mathrm{R} \\ $$$$\frac{\mathrm{P}}{\mathrm{P}_{\mathrm{0}} }\:=\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{P}\:=\:\frac{\mathrm{P}_{\mathrm{0}} }{\mathrm{4}}\:=\:\frac{\mathrm{569},\mathrm{37}}{\mathrm{4}}\:=\:\mathrm{142},\mathrm{34}\:\mathrm{N} \\ $$
Commented by aurpeyz last updated on 01/Aug/20
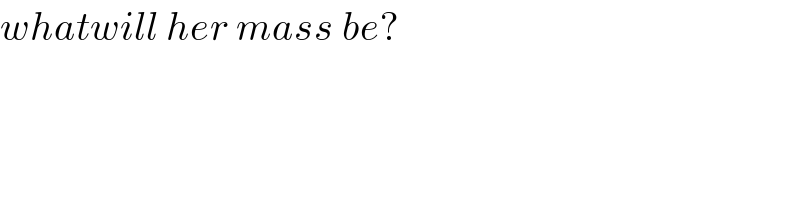
$${whatwill}\:{her}\:{mass}\:{be}? \\ $$
Answered by Dwaipayan Shikari last updated on 20/Jul/20
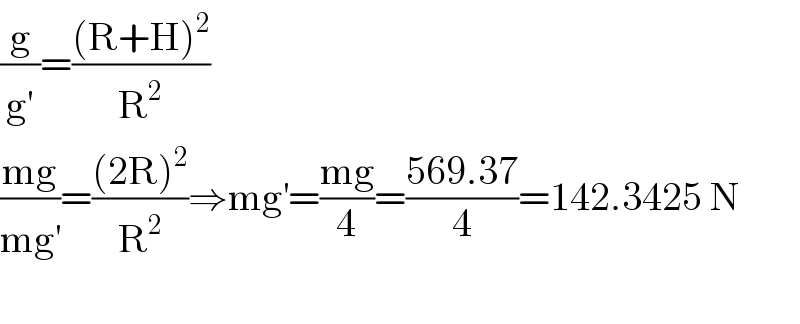
$$\frac{\mathrm{g}}{\mathrm{g}^{'} }=\frac{\left(\mathrm{R}+\mathrm{H}\right)^{\mathrm{2}} }{\mathrm{R}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{mg}}{\mathrm{mg}^{'} }=\frac{\left(\mathrm{2R}\right)^{\mathrm{2}} }{\mathrm{R}^{\mathrm{2}} }\Rightarrow\mathrm{mg}^{'} =\frac{\mathrm{mg}}{\mathrm{4}}=\frac{\mathrm{569}.\mathrm{37}}{\mathrm{4}}=\mathrm{142}.\mathrm{3425}\:\mathrm{N} \\ $$$$ \\ $$
Commented by aurpeyz last updated on 01/Aug/20
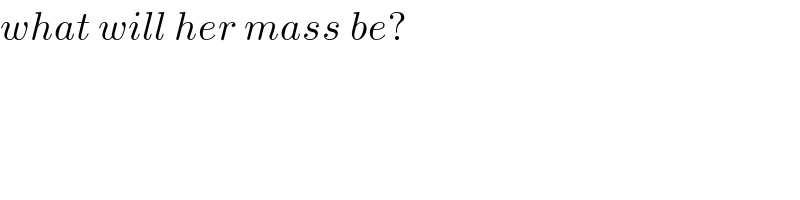
$${what}\:{will}\:{her}\:{mass}\:{be}? \\ $$
Commented by aurpeyz last updated on 01/Aug/20

$${pls}\:{help} \\ $$
