Question Number 27769 by tawa tawa last updated on 14/Jan/18

$$\mathrm{A}\:\mathrm{glass}\:\mathrm{bottle}\:\mathrm{full}\:\mathrm{of}\:\mathrm{mercury}\:\mathrm{has}\:\mathrm{mass}\:\mathrm{500g}.\:\mathrm{On}\:\mathrm{being}\:\mathrm{heated}\:\mathrm{through}\:\mathrm{35}°\mathrm{C}, \\ $$$$\mathrm{2}.\mathrm{43g}\:\mathrm{of}\:\mathrm{mercury}\:\mathrm{are}\:\mathrm{expelled}.\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{mercury}\:\mathrm{remaining}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{bottle}\:\:\left(\mathrm{Cubic}\:\mathrm{expansivity}\:\mathrm{of}\:\mathrm{mercury}\:\mathrm{is}\:\mathrm{1}.\mathrm{8}\:×\:\mathrm{10}^{−\mathrm{4}} \:\mathrm{per}\:\mathrm{K}.\right. \\ $$$$\mathrm{linear}\:\mathrm{expansivity}\:\mathrm{of}\:\mathrm{glass}\:\mathrm{is}\:\mathrm{8}.\mathrm{0}\:×\:\mathrm{10}^{−\mathrm{6}} \:\mathrm{per}\:\mathrm{K}. \\ $$
Answered by mrW2 last updated on 15/Jan/18
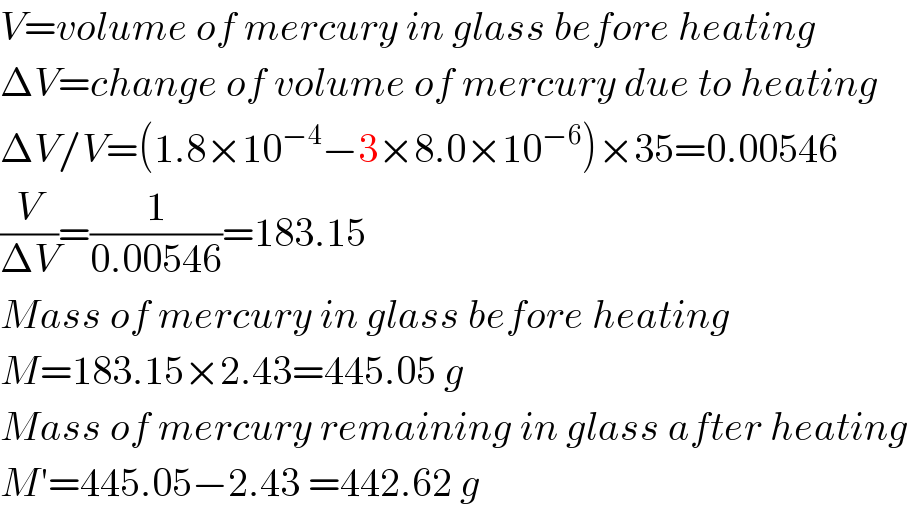
$${V}={volume}\:{of}\:{mercury}\:{in}\:{glass}\:{before}\:{heating} \\ $$$$\Delta{V}={change}\:{of}\:{volume}\:{of}\:{mercury}\:{due}\:{to}\:{heating} \\ $$$$\Delta{V}/{V}=\left(\mathrm{1}.\mathrm{8}×\mathrm{10}^{−\mathrm{4}} −\mathrm{3}×\mathrm{8}.\mathrm{0}×\mathrm{10}^{−\mathrm{6}} \right)×\mathrm{35}=\mathrm{0}.\mathrm{00546} \\ $$$$\frac{{V}}{\Delta{V}}=\frac{\mathrm{1}}{\mathrm{0}.\mathrm{00546}}=\mathrm{183}.\mathrm{15} \\ $$$${Mass}\:{of}\:{mercury}\:{in}\:{glass}\:{before}\:{heating} \\ $$$${M}=\mathrm{183}.\mathrm{15}×\mathrm{2}.\mathrm{43}=\mathrm{445}.\mathrm{05}\:{g} \\ $$$${Mass}\:{of}\:{mercury}\:{remaining}\:{in}\:{glass}\:{after}\:{heating} \\ $$$${M}'=\mathrm{445}.\mathrm{05}−\mathrm{2}.\mathrm{43}\:=\mathrm{442}.\mathrm{62}\:{g} \\ $$
Commented by tawa tawa last updated on 15/Jan/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
