Question Number 15418 by Tinkutara last updated on 10/Jun/17

$$\mathrm{A}\:\mathrm{grasshopper}\:\mathrm{can}\:\mathrm{jump}\:\mathrm{a}\:\mathrm{maximum} \\ $$$$\mathrm{horizontal}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{40}\:\mathrm{cm}.\:\mathrm{If}\:\mathrm{it} \\ $$$$\mathrm{spends}\:\mathrm{negligible}\:\mathrm{time}\:\mathrm{on}\:\mathrm{the}\:\mathrm{ground} \\ $$$$\mathrm{then}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{its}\:\mathrm{speed}\:\mathrm{along}\:\mathrm{the} \\ $$$$\mathrm{horizontal}\:\mathrm{road}\:\mathrm{will}\:\mathrm{be}? \\ $$
Answered by mrW1 last updated on 10/Jun/17
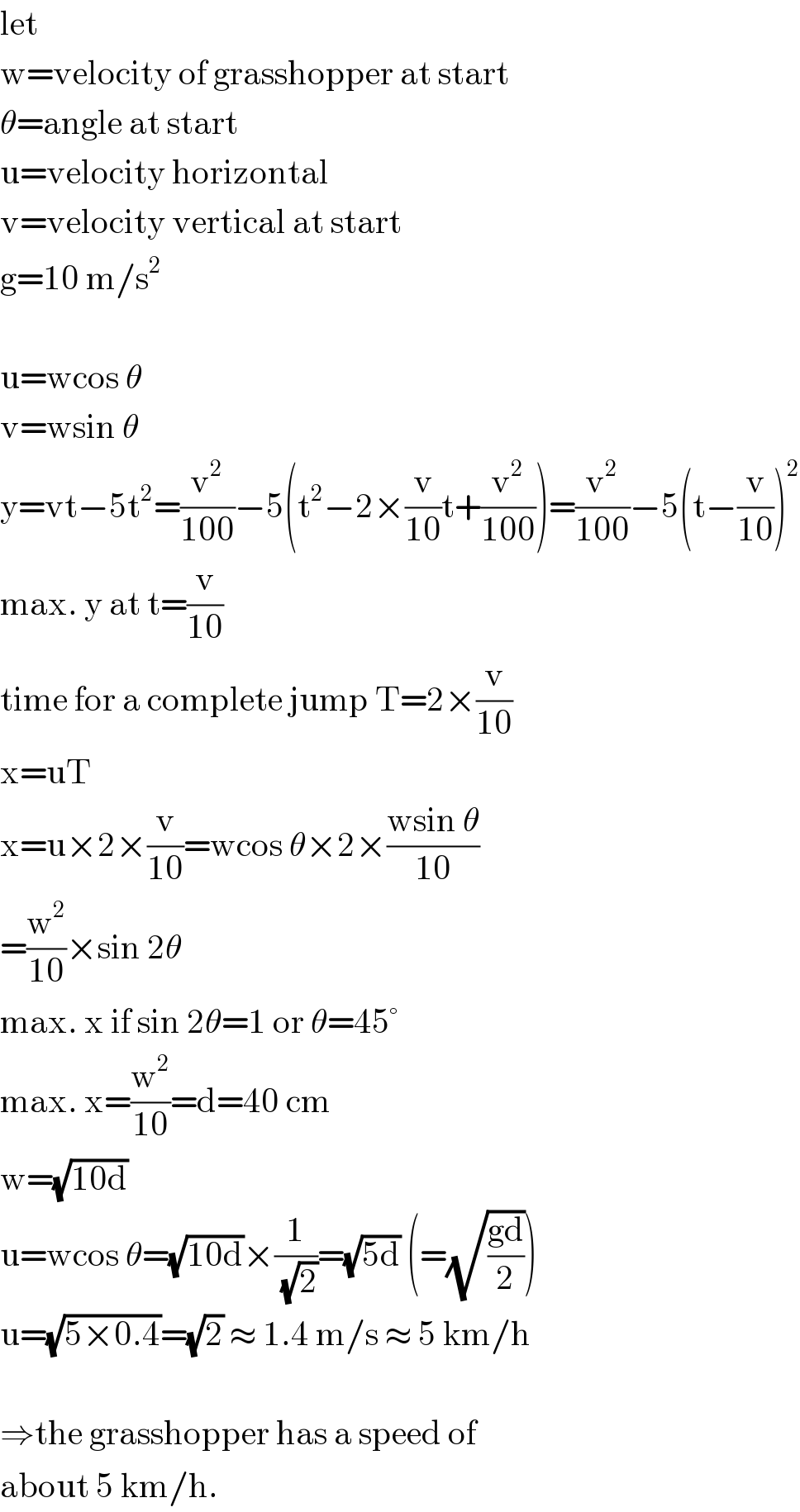
$$\mathrm{let} \\ $$$$\mathrm{w}=\mathrm{velocity}\:\mathrm{of}\:\mathrm{grasshopper}\:\mathrm{at}\:\mathrm{start} \\ $$$$\theta=\mathrm{angle}\:\mathrm{at}\:\mathrm{start} \\ $$$$\mathrm{u}=\mathrm{velocity}\:\mathrm{horizontal} \\ $$$$\mathrm{v}=\mathrm{velocity}\:\mathrm{vertical}\:\mathrm{at}\:\mathrm{start} \\ $$$$\mathrm{g}=\mathrm{10}\:\mathrm{m}/\mathrm{s}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{u}=\mathrm{wcos}\:\theta \\ $$$$\mathrm{v}=\mathrm{wsin}\:\theta \\ $$$$\mathrm{y}=\mathrm{vt}−\mathrm{5t}^{\mathrm{2}} =\frac{\mathrm{v}^{\mathrm{2}} }{\mathrm{100}}−\mathrm{5}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2}×\frac{\mathrm{v}}{\mathrm{10}}\mathrm{t}+\frac{\mathrm{v}^{\mathrm{2}} }{\mathrm{100}}\right)=\frac{\mathrm{v}^{\mathrm{2}} }{\mathrm{100}}−\mathrm{5}\left(\mathrm{t}−\frac{\mathrm{v}}{\mathrm{10}}\right)^{\mathrm{2}} \\ $$$$\mathrm{max}.\:\mathrm{y}\:\mathrm{at}\:\mathrm{t}=\frac{\mathrm{v}}{\mathrm{10}} \\ $$$$\mathrm{time}\:\mathrm{for}\:\mathrm{a}\:\mathrm{complete}\:\mathrm{jump}\:\mathrm{T}=\mathrm{2}×\frac{\mathrm{v}}{\mathrm{10}} \\ $$$$\mathrm{x}=\mathrm{uT} \\ $$$$\mathrm{x}=\mathrm{u}×\mathrm{2}×\frac{\mathrm{v}}{\mathrm{10}}=\mathrm{wcos}\:\theta×\mathrm{2}×\frac{\mathrm{wsin}\:\theta}{\mathrm{10}} \\ $$$$=\frac{\mathrm{w}^{\mathrm{2}} }{\mathrm{10}}×\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\mathrm{max}.\:\mathrm{x}\:\mathrm{if}\:\mathrm{sin}\:\mathrm{2}\theta=\mathrm{1}\:\mathrm{or}\:\theta=\mathrm{45}° \\ $$$$\mathrm{max}.\:\mathrm{x}=\frac{\mathrm{w}^{\mathrm{2}} }{\mathrm{10}}=\mathrm{d}=\mathrm{40}\:\mathrm{cm} \\ $$$$\mathrm{w}=\sqrt{\mathrm{10d}} \\ $$$$\mathrm{u}=\mathrm{wcos}\:\theta=\sqrt{\mathrm{10d}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\sqrt{\mathrm{5d}}\:\left(=\sqrt{\frac{\mathrm{gd}}{\mathrm{2}}}\right) \\ $$$$\mathrm{u}=\sqrt{\mathrm{5}×\mathrm{0}.\mathrm{4}}=\sqrt{\mathrm{2}}\:\approx\:\mathrm{1}.\mathrm{4}\:\mathrm{m}/\mathrm{s}\:\approx\:\mathrm{5}\:\mathrm{km}/\mathrm{h} \\ $$$$ \\ $$$$\Rightarrow\mathrm{the}\:\mathrm{grasshopper}\:\mathrm{has}\:\mathrm{a}\:\mathrm{speed}\:\mathrm{of} \\ $$$$\mathrm{about}\:\mathrm{5}\:\mathrm{km}/\mathrm{h}. \\ $$
Commented by Tinkutara last updated on 10/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by ajfour last updated on 10/Jun/17
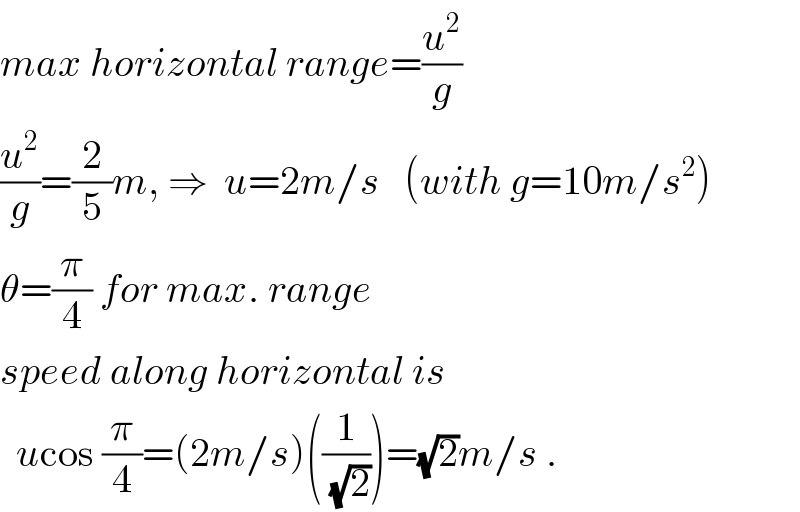
$${max}\:{horizontal}\:{range}=\frac{{u}^{\mathrm{2}} }{{g}} \\ $$$$\frac{{u}^{\mathrm{2}} }{{g}}=\frac{\mathrm{2}}{\mathrm{5}}{m},\:\Rightarrow\:\:{u}=\mathrm{2}{m}/{s}\:\:\:\left({with}\:{g}=\mathrm{10}{m}/{s}^{\mathrm{2}} \right) \\ $$$$\theta=\frac{\pi}{\mathrm{4}}\:{for}\:{max}.\:{range} \\ $$$${speed}\:{along}\:{horizontal}\:{is} \\ $$$$\:\:{u}\mathrm{cos}\:\frac{\pi}{\mathrm{4}}=\left(\mathrm{2}{m}/{s}\right)\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)=\sqrt{\mathrm{2}}{m}/{s}\:. \\ $$
Commented by Tinkutara last updated on 10/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
