Menu Close

a-gt-b-gt-0-a-2-cos-b-2-sin-a-2-b-2-sin-cos-Find-in-terms-of-a-b-0-pi-2-

Tinku Tara 0 Comments
Pin




Question Number 38151 by ajfour last updated on 22/Jun/18
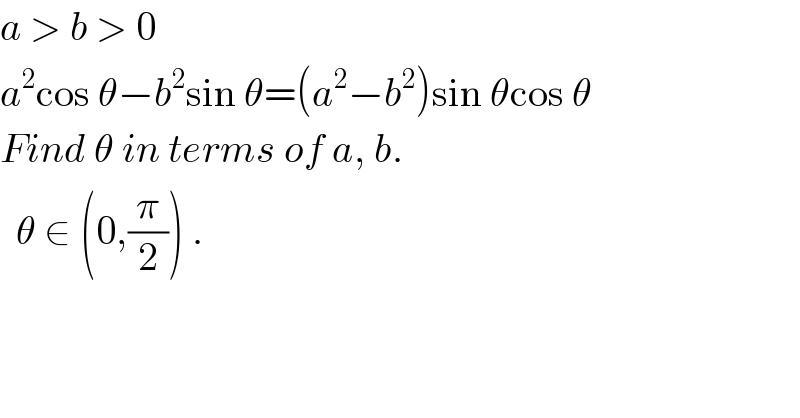
a > b > 0 a^2 cos θ−b^2 sin θ=(a^2 −b^2 )sin θcos θ Find θ in terms of a, b. θ ∈ (0,(π/2)) .
$${a}\:>\:{b}\:>\:\mathrm{0} \\ $$$${a}^{\mathrm{2}} \mathrm{cos}\:\theta−{b}^{\mathrm{2}} \mathrm{sin}\:\theta=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$${Find}\:\theta\:{in}\:{terms}\:{of}\:{a},\:{b}. \\ $$$$\:\:\theta\:\in\:\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right)\:. \\ $$
Commented by behi83417@gmail.com last updated on 23/Jun/18
let: m=e^(iθ) ,i=(√(−1)) ⇒a^2 .((m^2 +1)/(2m))−b^2 .((m^2 −1)/(2im))=(a^2 −b^2 )((m^4 −1)/(4im^2 )) ⇒2a^2 .m(m^2 +1)+2mib^2 (m^2 −1)=i(b^2 −a^2 )(m^4 −1) ⇒ { ((2a^2 .m(m^2 +1)=0 (A))),((2b^2 .m(m^2 −1)=(b^2 −a^2 )(m^4 −1) (B))) :} ⇒^A (a=0)∨(m=0)∨(m^2 +1)=0 a=0⇒cosθ=1⇒θ=0 ( ×) m=0⇒e^(iθ) =0 (×) m^2 +1=0⇒m=±i⇒e^(iθ) =e^(±i(π/2)) ⇒θ=±(π/2) (×) ⇒^B 2b^2 .m(m^2 −1)=(b^2 −a^2 )(m^4 −1) ⇒ { ((m^2 −1=0⇒m=±1⇒e^(iθ) =±1=e^(±iπ) )),((⇒θ=±π (×))) :}(×) 2b^2 .m=(b^2 −a^2 )(m^2 +1)⇒((m^2 +1)/(2m))=(b^2 /(b^2 −a^2 )) ((m^2 +1+2m)/(m^2 +1−2m))=((b^2 +b^2 −a^2 )/(b^2 −b^2 +a^2 ))⇒(((m+1)/(m−1)))^2 =2(b^2 /a^2 )−1 ⇒((m+1)/(m−1))=((√(2b^2 −a^2 ))/a)⇒((m+1+m−1)/(m+1−m+1))=(((√(2b^2 −a^2 ))+a)/( (√(2b^2 −a^2 ))−a)) ⇒m=((b^2 +a.(√(2b^2 −a^2 )))/(b^2 −a^2 )) ⇒e^(i𝛉) =((b^2 +a.(√(2b^2 −a^2 )))/(b^2 −a^2 )) ,(p=(b^2 /a^2 )) ⇒i𝛉=ln((b^2 +a(√(2b^2 −a^2 )))/(b^2 −a^2 )) ⇒i𝛉=ln((p+(√(2p−1)))/(p−1)) .■ =ln((p/(p−1))+((√(1−2p))/(p−1)).i)= =[(1/2)ln(((p^2 +(1−2p))/((p−1)^2 )))+i.arctg(((√(1−2p))/(p−1))/(p/(p−1)))]= =[(1/2)ln1+i.arctg((√(1−2p))/p)]=i.arctg((√(1−2p))/p) ⇒𝛉=arctg((√(1−2p))/p)=arctg((a.(√(a^2 −2b^2 )))/b^2 ).■ sir Ajfour! this is a real solution for your quistion.
$${let}:\:{m}={e}^{{i}\theta} \:\:\:,{i}=\sqrt{−\mathrm{1}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} .\frac{{m}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{m}}−{b}^{\mathrm{2}} .\frac{{m}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{im}}=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\frac{{m}^{\mathrm{4}} −\mathrm{1}}{\mathrm{4}{im}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2}{a}^{\mathrm{2}} .{m}\left({m}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{2}{mib}^{\mathrm{2}} \left({m}^{\mathrm{2}} −\mathrm{1}\right)={i}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({m}^{\mathrm{4}} −\mathrm{1}\right) \\ $$$$\Rightarrow\begin{cases}{\mathrm{2}{a}^{\mathrm{2}} .{m}\left({m}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0}\:\:\:\left({A}\right)}\\{\mathrm{2}{b}^{\mathrm{2}} .{m}\left({m}^{\mathrm{2}} −\mathrm{1}\right)=\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({m}^{\mathrm{4}} −\mathrm{1}\right)\:\left({B}\right)}\end{cases} \\ $$$$\overset{{A}} {\Rightarrow}\left({a}=\mathrm{0}\right)\vee\left({m}=\mathrm{0}\right)\vee\left({m}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$${a}=\mathrm{0}\Rightarrow{cos}\theta=\mathrm{1}\Rightarrow\theta=\mathrm{0}\:\left(\:×\right) \\ $$$${m}=\mathrm{0}\Rightarrow{e}^{{i}\theta} =\mathrm{0}\:\:\left(×\right) \\ $$$${m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\Rightarrow{m}=\pm{i}\Rightarrow{e}^{{i}\theta} ={e}^{\pm{i}\frac{\pi}{\mathrm{2}}} \Rightarrow\theta=\pm\frac{\pi}{\mathrm{2}}\:\left(×\right) \\ $$$$\overset{{B}} {\Rightarrow}\mathrm{2}{b}^{\mathrm{2}} .{m}\left({m}^{\mathrm{2}} −\mathrm{1}\right)=\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({m}^{\mathrm{4}} −\mathrm{1}\right) \\ $$$$\Rightarrow\begin{cases}{{m}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\Rightarrow{m}=\pm\mathrm{1}\Rightarrow{e}^{{i}\theta} =\pm\mathrm{1}={e}^{\pm{i}\pi} }\\{\Rightarrow\theta=\pm\pi\:\left(×\right)}\end{cases}\left(×\right) \\ $$$$\mathrm{2}{b}^{\mathrm{2}} .{m}=\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({m}^{\mathrm{2}} +\mathrm{1}\right)\Rightarrow\frac{{m}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{m}}=\frac{{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\frac{{m}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{m}}{{m}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{m}}=\frac{{b}^{\mathrm{2}} +{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} −{b}^{\mathrm{2}} +{a}^{\mathrm{2}} }\Rightarrow\left(\frac{{m}+\mathrm{1}}{{m}−\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{2}\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mathrm{1}\: \\ $$$$\Rightarrow\frac{{m}+\mathrm{1}}{{m}−\mathrm{1}}=\frac{\sqrt{\mathrm{2}{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}}\Rightarrow\frac{{m}+\mathrm{1}+{m}−\mathrm{1}}{{m}+\mathrm{1}−{m}+\mathrm{1}}=\frac{\sqrt{\mathrm{2}{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }+{a}}{\:\sqrt{\mathrm{2}{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }−{a}} \\ $$$$\Rightarrow\boldsymbol{{m}}=\frac{\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{a}}.\sqrt{\mathrm{2}\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} }}{\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} }\:\: \\ $$$$\Rightarrow\boldsymbol{{e}}^{\boldsymbol{{i}\theta}} =\frac{\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{a}}.\sqrt{\mathrm{2}\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} }}{\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} }\:\:\:\:,\left(\boldsymbol{{p}}=\frac{\boldsymbol{{b}}^{\mathrm{2}} }{\boldsymbol{{a}}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\boldsymbol{{i}\theta}=\boldsymbol{{ln}}\frac{\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{a}}\sqrt{\mathrm{2}\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} }}{\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} }\:\Rightarrow\boldsymbol{{i}\theta}=\boldsymbol{{ln}}\frac{\boldsymbol{{p}}+\sqrt{\mathrm{2}\boldsymbol{{p}}−\mathrm{1}}}{\boldsymbol{{p}}−\mathrm{1}}\:.\blacksquare \\ $$$$=\boldsymbol{{ln}}\left(\frac{\boldsymbol{{p}}}{\boldsymbol{{p}}−\mathrm{1}}+\frac{\sqrt{\mathrm{1}−\mathrm{2}\boldsymbol{{p}}}}{\boldsymbol{{p}}−\mathrm{1}}.\boldsymbol{{i}}\right)= \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{ln}}\left(\frac{\boldsymbol{{p}}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{2}\boldsymbol{{p}}\right)}{\left(\boldsymbol{{p}}−\mathrm{1}\right)^{\mathrm{2}} }\right)+\boldsymbol{{i}}.\boldsymbol{{arctg}}\frac{\frac{\sqrt{\mathrm{1}−\mathrm{2}\boldsymbol{{p}}}}{\boldsymbol{{p}}−\mathrm{1}}}{\frac{\boldsymbol{{p}}}{\boldsymbol{{p}}−\mathrm{1}}}\right]= \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{ln}}\mathrm{1}+\boldsymbol{{i}}.\boldsymbol{{arctg}}\frac{\sqrt{\mathrm{1}−\mathrm{2}\boldsymbol{{p}}}}{\boldsymbol{{p}}}\right]=\boldsymbol{{i}}.\boldsymbol{{arctg}}\frac{\sqrt{\mathrm{1}−\mathrm{2}\boldsymbol{{p}}}}{\boldsymbol{{p}}} \\ $$$$\Rightarrow\boldsymbol{\theta}=\boldsymbol{{arctg}}\frac{\sqrt{\mathrm{1}−\mathrm{2}\boldsymbol{{p}}}}{\boldsymbol{{p}}}=\boldsymbol{{arctg}}\frac{\boldsymbol{{a}}.\sqrt{\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{b}}^{\mathrm{2}} }}{\boldsymbol{{b}}^{\mathrm{2}} }.\blacksquare \\ $$$$\boldsymbol{{sir}}\:\boldsymbol{{Ajfour}}!\:\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{a}}\:\boldsymbol{{real}}\:\boldsymbol{{solution}} \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{your}}\:\boldsymbol{{quistion}}. \\ $$
Commented by ajfour last updated on 23/Jun/18
there has to be a real solution..
$${there}\:{has}\:{to}\:{be}\:{a}\:{real}\:{solution}.. \\ $$
Commented by MJS last updated on 23/Jun/18
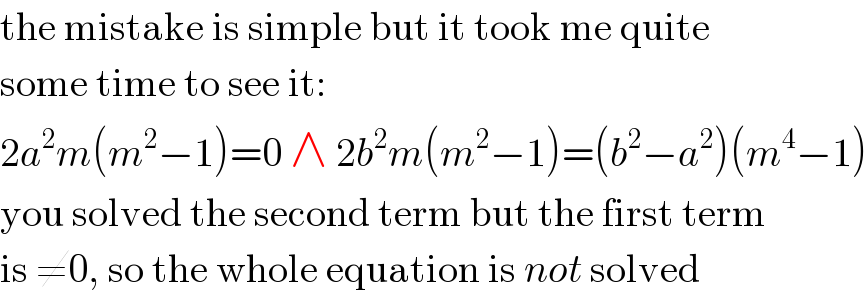
the mistake is simple but it took me quite some time to see it: 2a^2 m(m^2 −1)=0 ∧ 2b^2 m(m^2 −1)=(b^2 −a^2 )(m^4 −1) you solved the second term but the first term is ≠0, so the whole equation is not solved
$$\mathrm{the}\:\mathrm{mistake}\:\mathrm{is}\:\mathrm{simple}\:\mathrm{but}\:\mathrm{it}\:\mathrm{took}\:\mathrm{me}\:\mathrm{quite} \\ $$$$\mathrm{some}\:\mathrm{time}\:\mathrm{to}\:\mathrm{see}\:\mathrm{it}: \\ $$$$\mathrm{2}{a}^{\mathrm{2}} {m}\left({m}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0}\:\wedge\:\mathrm{2}{b}^{\mathrm{2}} {m}\left({m}^{\mathrm{2}} −\mathrm{1}\right)=\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({m}^{\mathrm{4}} −\mathrm{1}\right) \\ $$$$\mathrm{you}\:\mathrm{solved}\:\mathrm{the}\:\mathrm{second}\:\mathrm{term}\:\mathrm{but}\:\mathrm{the}\:\mathrm{first}\:\mathrm{term} \\ $$$$\mathrm{is}\:\neq\mathrm{0},\:\mathrm{so}\:\mathrm{the}\:\mathrm{whole}\:\mathrm{equation}\:\mathrm{is}\:{not}\:\mathrm{solved} \\ $$
Commented by behi83417@gmail.com last updated on 23/Jun/18
dear MJS! the 1#part of eq. is: 2a^2 .m(m^2 +1)=0 ,and it has solved.
$${dear}\:{MJS}!\:{the}\:\mathrm{1}#{part}\:{of}\:{eq}.\:{is}: \\ $$$$\:\:\:\:\:\:\mathrm{2}{a}^{\mathrm{2}} .{m}\left({m}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0}\:\:\:,{and}\:{it}\:{has}\:{solved}. \\ $$
Commented by MJS last updated on 23/Jun/18
sorry, typo. but have you tried your solution with any real numbers a and b? a=5 b=3 arctan (3^2 /( (√(5^2 −2×3^2 ))))=arctan ((9(√7))/7) 25cos arctan ((9(√7))/7) −9sin arctan ((9(√7))/7)= =((25(√(154)))/(44))−((81(√(22)))/(44))≈−1.58368 16sin arctan ((9(√7))/7) × cos arctan ((9(√7))/7)=((18(√7))/(11))≈4.32941 so something went wrong 25cos θ −9sin θ=16sin θ cos θ has the approximate solution 0.93305, while arctan ((9(√7))/7)≈1.2849
$$\mathrm{sorry},\:\mathrm{typo}. \\ $$$$\mathrm{but}\:\mathrm{have}\:\mathrm{you}\:\mathrm{tried}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{with}\:\mathrm{any} \\ $$$$\mathrm{real}\:\mathrm{numbers}\:{a}\:\mathrm{and}\:{b}? \\ $$$${a}=\mathrm{5} \\ $$$${b}=\mathrm{3} \\ $$$$\mathrm{arctan}\:\frac{\mathrm{3}^{\mathrm{2}} }{\:\sqrt{\mathrm{5}^{\mathrm{2}} −\mathrm{2}×\mathrm{3}^{\mathrm{2}} }}=\mathrm{arctan}\:\frac{\mathrm{9}\sqrt{\mathrm{7}}}{\mathrm{7}} \\ $$$$\mathrm{25cos}\:\mathrm{arctan}\:\frac{\mathrm{9}\sqrt{\mathrm{7}}}{\mathrm{7}}\:−\mathrm{9sin}\:\mathrm{arctan}\:\frac{\mathrm{9}\sqrt{\mathrm{7}}}{\mathrm{7}}= \\ $$$$=\frac{\mathrm{25}\sqrt{\mathrm{154}}}{\mathrm{44}}−\frac{\mathrm{81}\sqrt{\mathrm{22}}}{\mathrm{44}}\approx−\mathrm{1}.\mathrm{58368} \\ $$$$\mathrm{16sin}\:\mathrm{arctan}\:\frac{\mathrm{9}\sqrt{\mathrm{7}}}{\mathrm{7}}\:×\:\mathrm{cos}\:\mathrm{arctan}\:\frac{\mathrm{9}\sqrt{\mathrm{7}}}{\mathrm{7}}=\frac{\mathrm{18}\sqrt{\mathrm{7}}}{\mathrm{11}}\approx\mathrm{4}.\mathrm{32941} \\ $$$$\mathrm{so}\:\mathrm{something}\:\mathrm{went}\:\mathrm{wrong} \\ $$$$ \\ $$$$\mathrm{25cos}\:\theta\:−\mathrm{9sin}\:\theta=\mathrm{16sin}\:\theta\:\mathrm{cos}\:\theta\:\mathrm{has}\:\mathrm{the} \\ $$$$\mathrm{approximate}\:\mathrm{solution}\:\mathrm{0}.\mathrm{93305},\:\mathrm{while} \\ $$$$\mathrm{arctan}\:\frac{\mathrm{9}\sqrt{\mathrm{7}}}{\mathrm{7}}\approx\mathrm{1}.\mathrm{2849} \\ $$
Commented by MJS last updated on 23/Jun/18
sorry I misread still with this value the left side gives −26.523 but the righr side is −4.3294 and the new θ≈2.8557 while the solution is ≈.93305
$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{misread} \\ $$$$\mathrm{still}\:\mathrm{with}\:\mathrm{this}\:\mathrm{value}\:\mathrm{the}\:\mathrm{left}\:\mathrm{side}\:\mathrm{gives} \\ $$$$−\mathrm{26}.\mathrm{523} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{righr}\:\mathrm{side}\:\mathrm{is} \\ $$$$−\mathrm{4}.\mathrm{3294} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{new}\:\theta\approx\mathrm{2}.\mathrm{8557}\:\mathrm{while}\:\mathrm{the}\:\mathrm{solution} \\ $$$$\mathrm{is}\:\approx.\mathrm{93305} \\ $$
Commented by behi83417@gmail.com last updated on 23/Jun/18
dear MJS! please correct my typo or post correct answer. i know your answer will the best,finally.
$${dear}\:{MJS}!\:{please}\:{correct}\:{my}\:{typo}\:{or} \\ $$$${post}\:{correct}\:{answer}. \\ $$$${i}\:{know}\:{your}\:{answer}\:{will}\:{the}\:{best},{finally}. \\ $$
Commented by MJS last updated on 24/Jun/18
I didn′t mean to offend you, I just wanted to say there′s some mistake. the solution must solve the equation... we all should test our solutions with at least 2 or 3 sets of real numbers before posting them.
$$\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{mean}\:\mathrm{to}\:\mathrm{offend}\:\mathrm{you},\:\mathrm{I}\:\mathrm{just}\:\mathrm{wanted}\:\mathrm{to} \\ $$$$\mathrm{say}\:\mathrm{there}'\mathrm{s}\:\mathrm{some}\:\mathrm{mistake}.\:\mathrm{the}\:\mathrm{solution}\:\mathrm{must} \\ $$$$\mathrm{solve}\:\mathrm{the}\:\mathrm{equation}…\:\mathrm{we}\:\mathrm{all}\:\mathrm{should}\:\mathrm{test}\:\mathrm{our} \\ $$$$\mathrm{solutions}\:\mathrm{with}\:\mathrm{at}\:\mathrm{least}\:\mathrm{2}\:\mathrm{or}\:\mathrm{3}\:\mathrm{sets}\:\mathrm{of}\:\mathrm{real} \\ $$$$\mathrm{numbers}\:\mathrm{before}\:\mathrm{posting}\:\mathrm{them}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jun/18
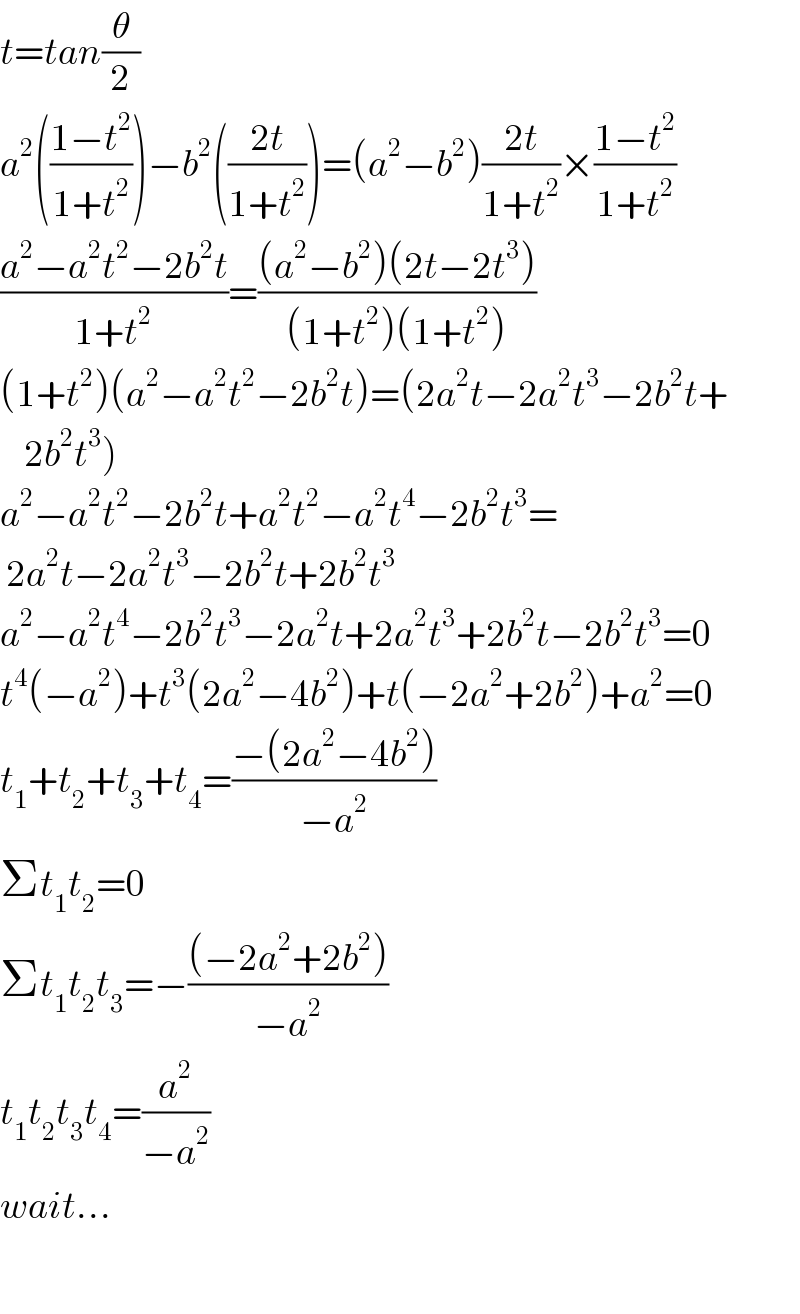
t=tan(θ/2) a^2 (((1−t^2 )/(1+t^2 )))−b^2 (((2t)/(1+t^2 )))=(a^2 −b^2 )((2t)/(1+t^2 ))×((1−t^2 )/(1+t^2 )) ((a^2 −a^2 t^2 −2b^2 t)/(1+t^2 ))=(((a^2 −b^2 )(2t−2t^3 ))/((1+t^2 )(1+t^2 ))) (1+t^2 )(a^2 −a^2 t^2 −2b^2 t)=(2a^2 t−2a^2 t^3 −2b^2 t+ 2b^2 t^3 ) a^2 −a^2 t^2 −2b^2 t+a^2 t^2 −a^2 t^4 −2b^2 t^3 = 2a^2 t−2a^2 t^3 −2b^2 t+2b^2 t^3 a^2 −a^2 t^4 −2b^2 t^3 −2a^2 t+2a^2 t^3 +2b^2 t−2b^2 t^3 =0 t^4 (−a^2 )+t^3 (2a^2 −4b^2 )+t(−2a^2 +2b^2 )+a^2 =0 t_1 +t_2 +t_3 +t_4 =((−(2a^2 −4b^2 ))/(−a^2 )) Σt_1 t_2 =0 Σt_1 t_2 t_3 =−(((−2a^2 +2b^2 ))/(−a^2 )) t_1 t_2 t_3 t_4 =(a^2 /(−a^2 )) wait...
$${t}={tan}\frac{\theta}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} \left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)−{b}^{\mathrm{2}} \left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\frac{{a}^{\mathrm{2}} −{a}^{\mathrm{2}} {t}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} {t}}{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left(\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{3}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} −{a}^{\mathrm{2}} {t}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} {t}\right)=\left(\mathrm{2}{a}^{\mathrm{2}} {t}−\mathrm{2}{a}^{\mathrm{2}} {t}^{\mathrm{3}} −\mathrm{2}{b}^{\mathrm{2}} {t}+\right. \\ $$$$\left.\:\:\:\:\mathrm{2}{b}^{\mathrm{2}} {t}^{\mathrm{3}} \right) \\ $$$${a}^{\mathrm{2}} −{a}^{\mathrm{2}} {t}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} {t}+{a}^{\mathrm{2}} {t}^{\mathrm{2}} −{a}^{\mathrm{2}} {t}^{\mathrm{4}} −\mathrm{2}{b}^{\mathrm{2}} {t}^{\mathrm{3}} = \\ $$$$\:\mathrm{2}{a}^{\mathrm{2}} {t}−\mathrm{2}{a}^{\mathrm{2}} {t}^{\mathrm{3}} −\mathrm{2}{b}^{\mathrm{2}} {t}+\mathrm{2}{b}^{\mathrm{2}} {t}^{\mathrm{3}} \\ $$$${a}^{\mathrm{2}} −{a}^{\mathrm{2}} {t}^{\mathrm{4}} −\mathrm{2}{b}^{\mathrm{2}} {t}^{\mathrm{3}} −\mathrm{2}{a}^{\mathrm{2}} {t}+\mathrm{2}{a}^{\mathrm{2}} {t}^{\mathrm{3}} +\mathrm{2}{b}^{\mathrm{2}} {t}−\mathrm{2}{b}^{\mathrm{2}} {t}^{\mathrm{3}} =\mathrm{0} \\ $$$${t}^{\mathrm{4}} \left(−{a}^{\mathrm{2}} \right)+{t}^{\mathrm{3}} \left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} \right)+{t}\left(−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${t}_{\mathrm{1}} +{t}_{\mathrm{2}} +{t}_{\mathrm{3}} +{t}_{\mathrm{4}} =\frac{−\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} \right)}{−{a}^{\mathrm{2}} } \\ $$$$\Sigma{t}_{\mathrm{1}} {t}_{\mathrm{2}} =\mathrm{0} \\ $$$$\Sigma{t}_{\mathrm{1}} {t}_{\mathrm{2}} {t}_{\mathrm{3}} =−\frac{\left(−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} \right)}{−{a}^{\mathrm{2}} } \\ $$$${t}_{\mathrm{1}} {t}_{\mathrm{2}} {t}_{\mathrm{3}} {t}_{\mathrm{4}} =\frac{{a}^{\mathrm{2}} }{−{a}^{\mathrm{2}} } \\ $$$${wait}… \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 22/Jun/18
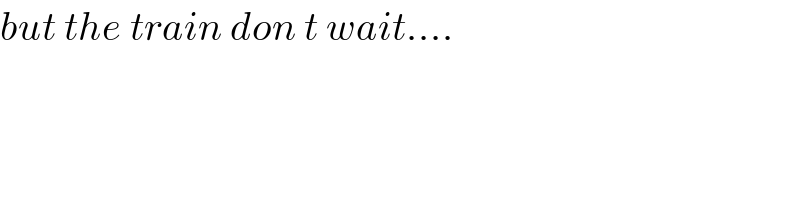
but the train don t wait....
$${but}\:{the}\:{train}\:{don}\:{t}\:{wait}…. \\ $$
Commented by rahul 19 last updated on 22/Jun/18
��������
Answered by ajfour last updated on 23/Jun/18
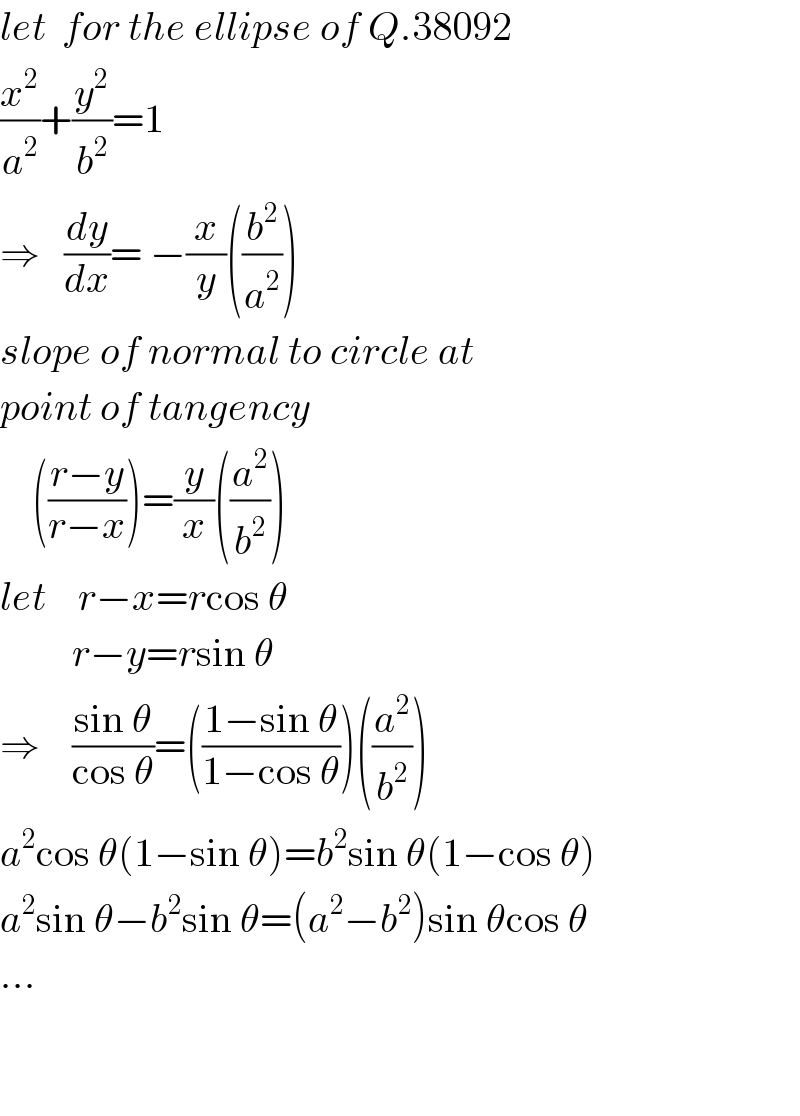
let for the ellipse of Q.38092 (x^2 /a^2 )+(y^2 /b^2 )=1 ⇒ (dy/dx)= −(x/y)((b^2 /a^2 )) slope of normal to circle at point of tangency (((r−y)/(r−x)))=(y/x)((a^2 /b^2 )) let r−x=rcos θ r−y=rsin θ ⇒ ((sin θ)/(cos θ))=(((1−sin θ)/(1−cos θ)))((a^2 /b^2 )) a^2 cos θ(1−sin θ)=b^2 sin θ(1−cos θ) a^2 sin θ−b^2 sin θ=(a^2 −b^2 )sin θcos θ ...
$${let}\:\:{for}\:{the}\:{ellipse}\:{of}\:{Q}.\mathrm{38092} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\:\:\:\frac{{dy}}{{dx}}=\:−\frac{{x}}{{y}}\left(\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$${slope}\:{of}\:{normal}\:{to}\:{circle}\:{at} \\ $$$${point}\:{of}\:{tangency} \\ $$$$\:\:\:\:\left(\frac{{r}−{y}}{{r}−{x}}\right)=\frac{{y}}{{x}}\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right) \\ $$$${let}\:\:\:\:{r}−{x}={r}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:{r}−{y}={r}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\:\:\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}=\left(\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{1}−\mathrm{cos}\:\theta}\right)\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right) \\ $$$${a}^{\mathrm{2}} \mathrm{cos}\:\theta\left(\mathrm{1}−\mathrm{sin}\:\theta\right)={b}^{\mathrm{2}} \mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$${a}^{\mathrm{2}} \mathrm{sin}\:\theta−{b}^{\mathrm{2}} \mathrm{sin}\:\theta=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$$… \\ $$$$ \\ $$$$ \\ $$
Answered by MJS last updated on 25/Jun/18
it′s not nice and probably not useable but it′s possible let a=1 and b^2 =q (q=(b^2 /a^2 )) cos θ −qsin θ −(1−q)sin θ cos θ =0 θ=2arctan t −((t^4 +2(2q−1)t^3 +2t−1)/(t^4 +2t^2 +1))=0 t^4 +2t+1=0 ⇒ t=±i ∉R ⇒ we can multiplicate without further trouble t^4 +2(2q−1)t^3 +2t−1=0 approximate solving with some values of q leads to the conclusion that this has two complex and two real solutions. the complex ones must be α+βi and α−βi and I hope the real ones are γ+δ and γ−δ. (t−α−βi)(t−α+βi)(t−γ−δ)(t−γ+δ)=0 t^4 − −2(α+γ)t^3 + +(α^2 +4ϑγ+β^2 +γ^2 −δ^2 )t^2 − −2(α^2 γ+αγ^2 −αδ^2 +β^2 γ)t+ +(α^2 +β^2 )(γ^2 −δ^2 )=0 ⇒ [1] 2(2q−1)=−2(α+γ) [2] 0=α^2 +4ϑγ+β^2 +γ^2 −δ^2 [3] 2=−2(α^2 γ+αγ^2 −αδ^2 +β^2 γ) [4] −1=(α^2 +β^2 )(γ^2 −δ^2 ) [1] α=−γ−2q+1 [2] β=(√(−α^2 −4αγ−γ^2 +δ^2 ))= =(√(2γ^2 +(4q−2)γ+δ^2 −(2q−1)^2 )) [3] 2=−4γ^3 +(6−12q)γ^2 −2(2γ+2q−1)δ^2 ⇒ ⇒ δ=(√(−((2γ^3 +3(2q−1)γ^2 +1)/(2γ+2q−1)))) ⇒ β=(√((2γ^3 +3(2q−1)γ^2 −2q(4q^2 −6q+3))/(2γ+2q−1))) [4] −1=((16γ^6 +48(2q−1)γ^5 +48(2q−1)^2 γ^4 +16(2q−1)^3 γ^3 +4(2q−1)γ^2 +4(2q−1)^2 γ−1)/((2γ+2q−1)^2 )) [γ≠(1/2)−q; this will be fulfilled with q=((1−(2)^(1/3) )/2)<0 so we don′t have to care] γ^6 +3(2q−1)γ^5 +3(2q−1)^2 γ^4 +(2q−1)^3 γ^3 +(q/2)γ^2 +((q(2q−1))/2)γ+((q(q−1))/4)=0 at this point we can only try to omit the γ^5 by setting γ=u−((3(2q−1))/6)=u−q+(1/2) which leads to u^6 −((3(2q−1)^2 )/4)u^4 +((48q^4 −96q^3 +72q^2 −16q+3)/(16))u^2 −(((8q^3 −12q^2 +6q+1)^2 )/(64))=0 we seem to have good luck set u=(√v) v^3 −((3(2q−1)^2 )/4)v^2 +((48q^4 −96q^3 +72q^2 −16q+3)/(16))v−(((8q^3 −12q^2 +6q+1)^2 )/(64))=0 omit v^2 by setting v=w−(((2q−1)^2 )/4) leads to w^3 +(q/2)w+((q(q−1))/4)=0 [x^3 +Px+Q=0 ⇒ ⇒ x_1 =((−(Q/2)+(√((P^3 /(27))+(Q^2 /4)))))^(1/3) +((−(Q/2)−(√((P^3 /(27))+(Q^2 /4)))))^(1/3) ] w_1 =((q)^(1/3) /2)(((1−q+(√((q−1)^2 +((8q)/(27))))))^(1/3) +((1−q−(√((q−1)^2 +((8q)/(27))))))^(1/3) ) (q−1)^2 +((8q)/(27))>0 ∀q>0 ⇒ w_1 ∈R ∀ q>0 ...now we have to set q and go all the way back... solutions of polynomes of 4^(th) degree usually are even worse...
$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{nice}\:\mathrm{and}\:\mathrm{probably}\:\mathrm{not}\:\mathrm{useable}\:\mathrm{but} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{possible} \\ $$$$\mathrm{let}\:{a}=\mathrm{1}\:\mathrm{and}\:{b}^{\mathrm{2}} ={q}\:\left({q}=\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\mathrm{cos}\:\theta\:−{q}\mathrm{sin}\:\theta\:−\left(\mathrm{1}−{q}\right)\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:=\mathrm{0} \\ $$$$\theta=\mathrm{2arctan}\:{t} \\ $$$$−\frac{{t}^{\mathrm{4}} +\mathrm{2}\left(\mathrm{2}{q}−\mathrm{1}\right){t}^{\mathrm{3}} +\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$${t}^{\mathrm{4}} +\mathrm{2}{t}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:{t}=\pm\mathrm{i}\:\notin\mathbb{R}\:\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{multiplicate} \\ $$$$\:\:\:\:\:\mathrm{without}\:\mathrm{further}\:\mathrm{trouble} \\ $$$${t}^{\mathrm{4}} +\mathrm{2}\left(\mathrm{2}{q}−\mathrm{1}\right){t}^{\mathrm{3}} +\mathrm{2}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{approximate}\:\mathrm{solving}\:\mathrm{with}\:\mathrm{some}\:\mathrm{values}\:\mathrm{of}\:{q} \\ $$$$\mathrm{leads}\:\mathrm{to}\:\mathrm{the}\:\mathrm{conclusion}\:\mathrm{that}\:\mathrm{this}\:\mathrm{has}\:\mathrm{two} \\ $$$$\mathrm{complex}\:\mathrm{and}\:\mathrm{two}\:\mathrm{real}\:\mathrm{solutions}.\:\mathrm{the}\:\mathrm{complex} \\ $$$$\mathrm{ones}\:\mathrm{must}\:\mathrm{be}\:\alpha+\beta\mathrm{i}\:\mathrm{and}\:\alpha−\beta\mathrm{i}\:\mathrm{and}\:\mathrm{I}\:\mathrm{hope}\:\mathrm{the} \\ $$$$\mathrm{real}\:\mathrm{ones}\:\mathrm{are}\:\gamma+\delta\:\mathrm{and}\:\gamma−\delta. \\ $$$$\left({t}−\alpha−\beta\mathrm{i}\right)\left({t}−\alpha+\beta\mathrm{i}\right)\left({t}−\gamma−\delta\right)\left({t}−\gamma+\delta\right)=\mathrm{0} \\ $$$${t}^{\mathrm{4}} − \\ $$$$\:\:\:\:\:−\mathrm{2}\left(\alpha+\gamma\right){t}^{\mathrm{3}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:+\left(\alpha^{\mathrm{2}} +\mathrm{4}\vartheta\gamma+\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} −\delta^{\mathrm{2}} \right){t}^{\mathrm{2}} − \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}\left(\alpha^{\mathrm{2}} \gamma+\alpha\gamma^{\mathrm{2}} −\alpha\delta^{\mathrm{2}} +\beta^{\mathrm{2}} \gamma\right){t}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\left(\gamma^{\mathrm{2}} −\delta^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\left[\mathrm{1}\right]\:\mathrm{2}\left(\mathrm{2}{q}−\mathrm{1}\right)=−\mathrm{2}\left(\alpha+\gamma\right) \\ $$$$\left[\mathrm{2}\right]\:\mathrm{0}=\alpha^{\mathrm{2}} +\mathrm{4}\vartheta\gamma+\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} −\delta^{\mathrm{2}} \\ $$$$\left[\mathrm{3}\right]\:\mathrm{2}=−\mathrm{2}\left(\alpha^{\mathrm{2}} \gamma+\alpha\gamma^{\mathrm{2}} −\alpha\delta^{\mathrm{2}} +\beta^{\mathrm{2}} \gamma\right) \\ $$$$\left[\mathrm{4}\right]\:−\mathrm{1}=\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)\left(\gamma^{\mathrm{2}} −\delta^{\mathrm{2}} \right) \\ $$$$ \\ $$$$\left[\mathrm{1}\right]\:\alpha=−\gamma−\mathrm{2}{q}+\mathrm{1} \\ $$$$\left[\mathrm{2}\right]\:\beta=\sqrt{−\alpha^{\mathrm{2}} −\mathrm{4}\alpha\gamma−\gamma^{\mathrm{2}} +\delta^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}\gamma^{\mathrm{2}} +\left(\mathrm{4}{q}−\mathrm{2}\right)\gamma+\delta^{\mathrm{2}} −\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left[\mathrm{3}\right]\:\mathrm{2}=−\mathrm{4}\gamma^{\mathrm{3}} +\left(\mathrm{6}−\mathrm{12}{q}\right)\gamma^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}\gamma+\mathrm{2}{q}−\mathrm{1}\right)\delta^{\mathrm{2}} \:\Rightarrow \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\delta=\sqrt{−\frac{\mathrm{2}\gamma^{\mathrm{3}} +\mathrm{3}\left(\mathrm{2}{q}−\mathrm{1}\right)\gamma^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}\gamma+\mathrm{2}{q}−\mathrm{1}}} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\beta=\sqrt{\frac{\mathrm{2}\gamma^{\mathrm{3}} +\mathrm{3}\left(\mathrm{2}{q}−\mathrm{1}\right)\gamma^{\mathrm{2}} −\mathrm{2}{q}\left(\mathrm{4}{q}^{\mathrm{2}} −\mathrm{6}{q}+\mathrm{3}\right)}{\mathrm{2}\gamma+\mathrm{2}{q}−\mathrm{1}}} \\ $$$$\left[\mathrm{4}\right]\:−\mathrm{1}=\frac{\mathrm{16}\gamma^{\mathrm{6}} +\mathrm{48}\left(\mathrm{2}{q}−\mathrm{1}\right)\gamma^{\mathrm{5}} +\mathrm{48}\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{2}} \gamma^{\mathrm{4}} +\mathrm{16}\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{3}} \gamma^{\mathrm{3}} +\mathrm{4}\left(\mathrm{2}{q}−\mathrm{1}\right)\gamma^{\mathrm{2}} +\mathrm{4}\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{2}} \gamma−\mathrm{1}}{\left(\mathrm{2}\gamma+\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left[\gamma\neq\frac{\mathrm{1}}{\mathrm{2}}−{q};\:\mathrm{this}\:\mathrm{will}\:\mathrm{be}\:\mathrm{fulfilled}\:\mathrm{with}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:{q}=\frac{\mathrm{1}−\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}<\mathrm{0}\:\mathrm{so}\:\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{to}\:\mathrm{care}\right] \\ $$$$\:\:\:\:\:\:\:\:\gamma^{\mathrm{6}} +\mathrm{3}\left(\mathrm{2}{q}−\mathrm{1}\right)\gamma^{\mathrm{5}} +\mathrm{3}\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{2}} \gamma^{\mathrm{4}} +\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{3}} \gamma^{\mathrm{3}} +\frac{{q}}{\mathrm{2}}\gamma^{\mathrm{2}} +\frac{{q}\left(\mathrm{2}{q}−\mathrm{1}\right)}{\mathrm{2}}\gamma+\frac{{q}\left({q}−\mathrm{1}\right)}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{at}\:\mathrm{this}\:\mathrm{point}\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{try}\:\mathrm{to}\:\mathrm{omit}\:\mathrm{the}\:\gamma^{\mathrm{5}} \\ $$$$\mathrm{by}\:\mathrm{setting}\:\gamma={u}−\frac{\mathrm{3}\left(\mathrm{2}{q}−\mathrm{1}\right)}{\mathrm{6}}={u}−{q}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{which}\:\mathrm{leads}\:\mathrm{to} \\ $$$${u}^{\mathrm{6}} −\frac{\mathrm{3}\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}{u}^{\mathrm{4}} +\frac{\mathrm{48}{q}^{\mathrm{4}} −\mathrm{96}{q}^{\mathrm{3}} +\mathrm{72}{q}^{\mathrm{2}} −\mathrm{16}{q}+\mathrm{3}}{\mathrm{16}}{u}^{\mathrm{2}} −\frac{\left(\mathrm{8}{q}^{\mathrm{3}} −\mathrm{12}{q}^{\mathrm{2}} +\mathrm{6}{q}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{64}}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{have}\:\mathrm{good}\:\mathrm{luck} \\ $$$$\mathrm{set}\:{u}=\sqrt{{v}} \\ $$$${v}^{\mathrm{3}} −\frac{\mathrm{3}\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}{v}^{\mathrm{2}} +\frac{\mathrm{48}{q}^{\mathrm{4}} −\mathrm{96}{q}^{\mathrm{3}} +\mathrm{72}{q}^{\mathrm{2}} −\mathrm{16}{q}+\mathrm{3}}{\mathrm{16}}{v}−\frac{\left(\mathrm{8}{q}^{\mathrm{3}} −\mathrm{12}{q}^{\mathrm{2}} +\mathrm{6}{q}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{64}}=\mathrm{0} \\ $$$$\mathrm{omit}\:{v}^{\mathrm{2}} \:\mathrm{by}\:\mathrm{setting}\:{v}={w}−\frac{\left(\mathrm{2}{q}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\:\mathrm{leads}\:\mathrm{to} \\ $$$${w}^{\mathrm{3}} +\frac{{q}}{\mathrm{2}}{w}+\frac{{q}\left({q}−\mathrm{1}\right)}{\mathrm{4}}=\mathrm{0} \\ $$$$\:\:\:\:\:\left[{x}^{\mathrm{3}} +\mathcal{P}{x}+\mathcal{Q}=\mathrm{0}\:\Rightarrow\right. \\ $$$$\left.\:\:\:\:\:\:\Rightarrow\:{x}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{−\frac{\mathcal{Q}}{\mathrm{2}}+\sqrt{\frac{\mathcal{P}^{\mathrm{3}} }{\mathrm{27}}+\frac{\mathcal{Q}^{\mathrm{2}} }{\mathrm{4}}}}+\sqrt[{\mathrm{3}}]{−\frac{\mathcal{Q}}{\mathrm{2}}−\sqrt{\frac{\mathcal{P}^{\mathrm{3}} }{\mathrm{27}}+\frac{\mathcal{Q}^{\mathrm{2}} }{\mathrm{4}}}}\right] \\ $$$${w}_{\mathrm{1}} =\frac{\sqrt[{\mathrm{3}}]{{q}}}{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\mathrm{1}−{q}+\sqrt{\left({q}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{8}{q}}{\mathrm{27}}}}+\sqrt[{\mathrm{3}}]{\mathrm{1}−{q}−\sqrt{\left({q}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{8}{q}}{\mathrm{27}}}}\right) \\ $$$$\left({q}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{8}{q}}{\mathrm{27}}>\mathrm{0}\:\forall{q}>\mathrm{0}\:\Rightarrow\:{w}_{\mathrm{1}} \in\mathbb{R}\:\forall\:{q}>\mathrm{0} \\ $$$$…\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{set}\:{q}\:\mathrm{and}\:\mathrm{go}\:\mathrm{all}\:\mathrm{the}\:\mathrm{way} \\ $$$$\mathrm{back}…\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{polynomes}\:\mathrm{of}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree} \\ $$$$\mathrm{usually}\:\mathrm{are}\:\mathrm{even}\:\mathrm{worse}… \\ $$
Commented by ajfour last updated on 25/Jun/18
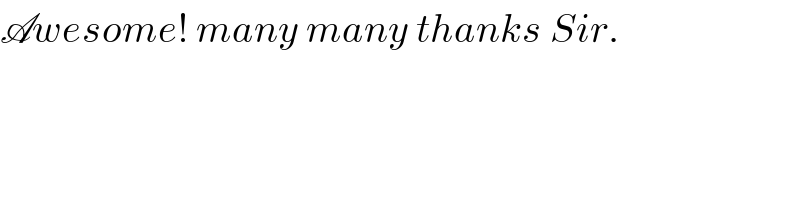
Awesome! many many thanks Sir.
$$\mathscr{A}{wesome}!\:{many}\:{many}\:{thanks}\:{Sir}. \\ $$
Commented by MJS last updated on 25/Jun/18
you won′t be able to use this for further simplifications or transformations but at least it′s possible to calculate approximate values using a calculator... by the way, it seems β and δ are imaginary numbers, so α±βi will be real and γ±δ will be complex...
$$\mathrm{you}\:\mathrm{won}'\mathrm{t}\:\mathrm{be}\:\mathrm{able}\:\mathrm{to}\:\mathrm{use}\:\mathrm{this}\:\mathrm{for}\:\mathrm{further} \\ $$$$\mathrm{simplifications}\:\mathrm{or}\:\mathrm{transformations}\:\mathrm{but}\:\mathrm{at} \\ $$$$\mathrm{least}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{approximate} \\ $$$$\mathrm{values}\:\mathrm{using}\:\mathrm{a}\:\mathrm{calculator}… \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{way},\:\mathrm{it}\:\mathrm{seems}\:\beta\:\mathrm{and}\:\delta\:\mathrm{are}\:\mathrm{imaginary} \\ $$$$\mathrm{numbers},\:\mathrm{so}\:\alpha\pm\beta\mathrm{i}\:\mathrm{will}\:\mathrm{be}\:\mathrm{real}\:\mathrm{and}\:\gamma\pm\delta\:\mathrm{will} \\ $$$$\mathrm{be}\:\mathrm{complex}… \\ $$
Commented by MJS last updated on 25/Jun/18
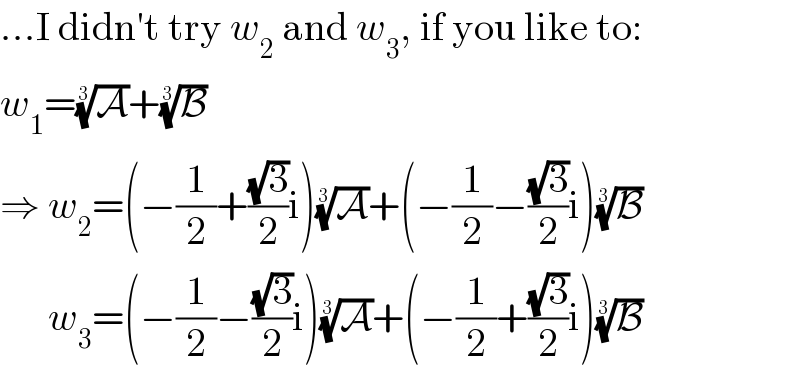
...I didn′t try w_2 and w_3 , if you like to: w_1 =(A)^(1/3) +(B)^(1/3) ⇒ w_2 =(−(1/2)+((√3)/2)i)(A)^(1/3) +(−(1/2)−((√3)/2)i)(B)^(1/3) w_3 =(−(1/2)−((√3)/2)i)(A)^(1/3) +(−(1/2)+((√3)/2)i)(B)^(1/3)
$$…\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{try}\:{w}_{\mathrm{2}} \:\mathrm{and}\:{w}_{\mathrm{3}} ,\:\mathrm{if}\:\mathrm{you}\:\mathrm{like}\:\mathrm{to}: \\ $$$${w}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{\mathcal{A}}+\sqrt[{\mathrm{3}}]{\mathcal{B}} \\ $$$$\Rightarrow\:{w}_{\mathrm{2}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\sqrt[{\mathrm{3}}]{\mathcal{A}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\sqrt[{\mathrm{3}}]{\mathcal{B}} \\ $$$$\:\:\:\:\:\:{w}_{\mathrm{3}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\sqrt[{\mathrm{3}}]{\mathcal{A}}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\sqrt[{\mathrm{3}}]{\mathcal{B}} \\ $$
Commented by ajfour last updated on 26/Jun/18
I got it reduced to a cubic eq. quite easily, i shall share that soon..
$${I}\:{got}\:{it}\:{reduced}\:{to}\:{a}\:{cubic}\:{eq}. \\ $$$${quite}\:{easily},\:{i}\:{shall}\:{share}\:{that} \\ $$$${soon}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *