Question Number 144909 by ArielVyny last updated on 30/Jun/21
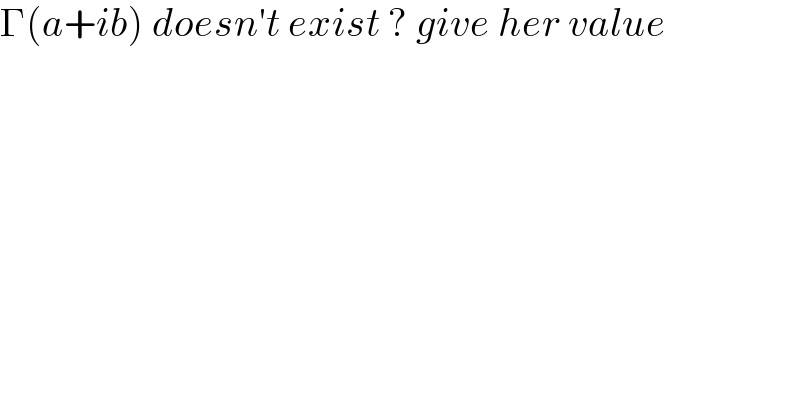
$$\Gamma\left({a}+{ib}\right)\:{doesn}'{t}\:{exist}\:?\:{give}\:{her}\:{value} \\ $$
Answered by qaz last updated on 30/Jun/21
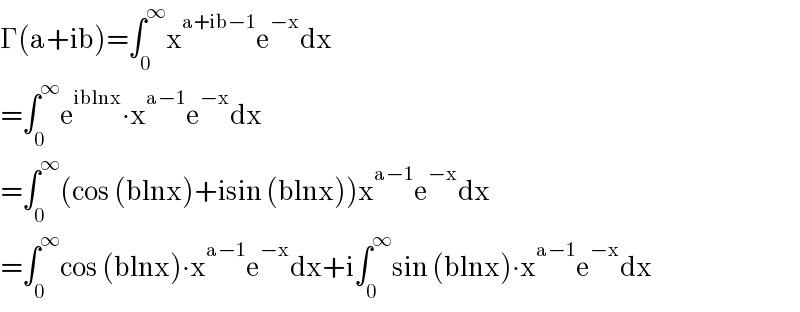
$$\Gamma\left(\mathrm{a}+\mathrm{ib}\right)=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{a}+\mathrm{ib}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\mathrm{iblnx}} \centerdot\mathrm{x}^{\mathrm{a}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{cos}\:\left(\mathrm{blnx}\right)+\mathrm{isin}\:\left(\mathrm{blnx}\right)\right)\mathrm{x}^{\mathrm{a}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathrm{cos}\:\left(\mathrm{blnx}\right)\centerdot\mathrm{x}^{\mathrm{a}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx}+\mathrm{i}\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\:\left(\mathrm{blnx}\right)\centerdot\mathrm{x}^{\mathrm{a}−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} \mathrm{dx} \\ $$
