Question Number 46474 by peter frank last updated on 28/Oct/18

$$\left.\mathrm{a}\right)\left[\mathrm{If}\:\mathrm{tan}^{−\mathrm{1}} \mathrm{a}+\mathrm{tan}^{−\mathrm{1}} \mathrm{b}+\mathrm{tan}^{−\mathrm{1}} \mathrm{c}=\pi\:\:\mathrm{show}\:\mathrm{that}\:\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{abc}}=\mathrm{1}\right. \\ $$$$\left.\mathrm{b}\right)\left[\:\:\mathrm{If}\:\:\mathrm{tanx}=\frac{\mathrm{nsinycosy}}{\mathrm{1}−\mathrm{nsin}^{\mathrm{2}} \mathrm{y}}\right. \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{tan}\left(\mathrm{y}−\mathrm{x}\right)=\left(\mathrm{1}−\mathrm{n}\right)\mathrm{tany} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by math1967 last updated on 27/Oct/18

$${pls}.{check}\:{q}\left({a}\right) \\ $$
Commented by peter frank last updated on 28/Oct/18

$$\mathrm{ready}\:\mathrm{sir} \\ $$
Answered by math1967 last updated on 27/Oct/18
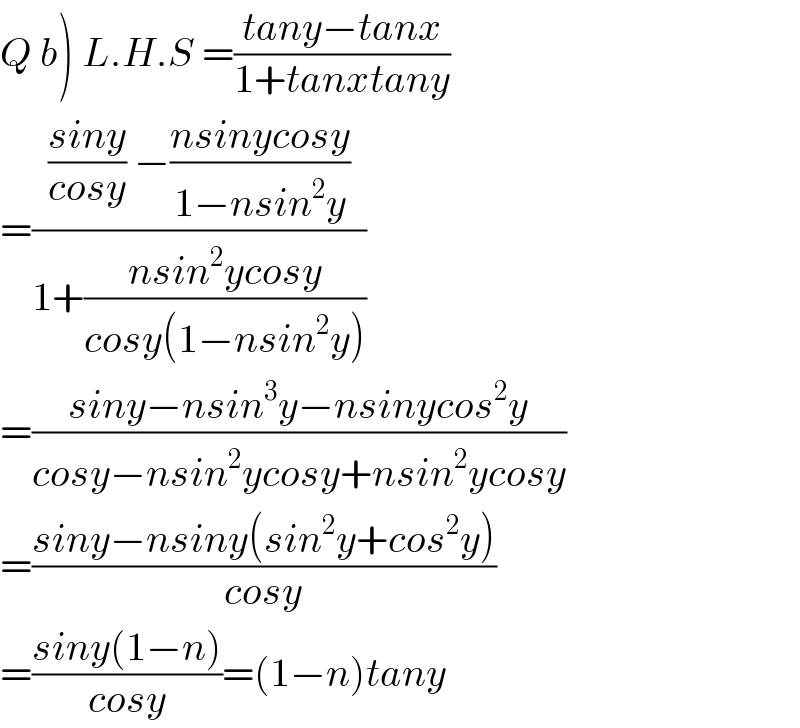
$$\left.{Q}\:{b}\right)\:{L}.{H}.{S}\:=\frac{{tany}−{tanx}}{\mathrm{1}+{tanxtany}} \\ $$$$=\frac{\frac{{siny}}{{cosy}}\:−\frac{{nsinycosy}}{\mathrm{1}−{nsin}^{\mathrm{2}} {y}}}{\mathrm{1}+\frac{{nsin}^{\mathrm{2}} {ycosy}}{{cosy}\left(\mathrm{1}−{nsin}^{\mathrm{2}} {y}\right)}} \\ $$$$=\frac{{siny}−{nsin}^{\mathrm{3}} {y}−{nsinycos}^{\mathrm{2}} {y}}{{cosy}−{nsin}^{\mathrm{2}} {ycosy}+{nsin}^{\mathrm{2}} {ycosy}} \\ $$$$=\frac{{siny}−{nsiny}\left({sin}^{\mathrm{2}} {y}+{cos}^{\mathrm{2}} {y}\right)}{{cosy}}\:\: \\ $$$$=\frac{{siny}\left(\mathrm{1}−{n}\right)}{{cosy}}=\left(\mathrm{1}−{n}\right){tany} \\ $$
Answered by math1967 last updated on 28/Oct/18

$${let}\mathrm{tan}^{−\mathrm{1}} {a}=\alpha,\:\mathrm{tan}^{−\mathrm{1}} {b}=\beta\:,\mathrm{tan}^{−\mathrm{1}} {c}=\gamma \\ $$$$\:{a}=\mathrm{tan}\:\alpha\:,{b}=\mathrm{tan}\:\beta,{c}=\mathrm{tan}\:\gamma \\ $$$${Again}\:\alpha+\beta+\gamma=\pi \\ $$$$\:\alpha+\beta=\pi−\gamma \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\mathrm{tan}\:\left(\pi−\gamma\right) \\ $$$$\frac{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\alpha\mathrm{tan}\:\beta}=−\mathrm{tan}\:\gamma \\ $$$$\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta=−\mathrm{tan}\:\gamma+\mathrm{tan}\:\alpha\mathrm{tan}\:\beta\mathrm{tan}\:\gamma \\ $$$$\therefore{a}+{b}+{c}={abc} \\ $$$$\therefore\frac{{a}+{b}+{c}}{{abc}}=\mathrm{1}\:{proved} \\ $$
