Question Number 63536 by Rio Michael last updated on 05/Jul/19
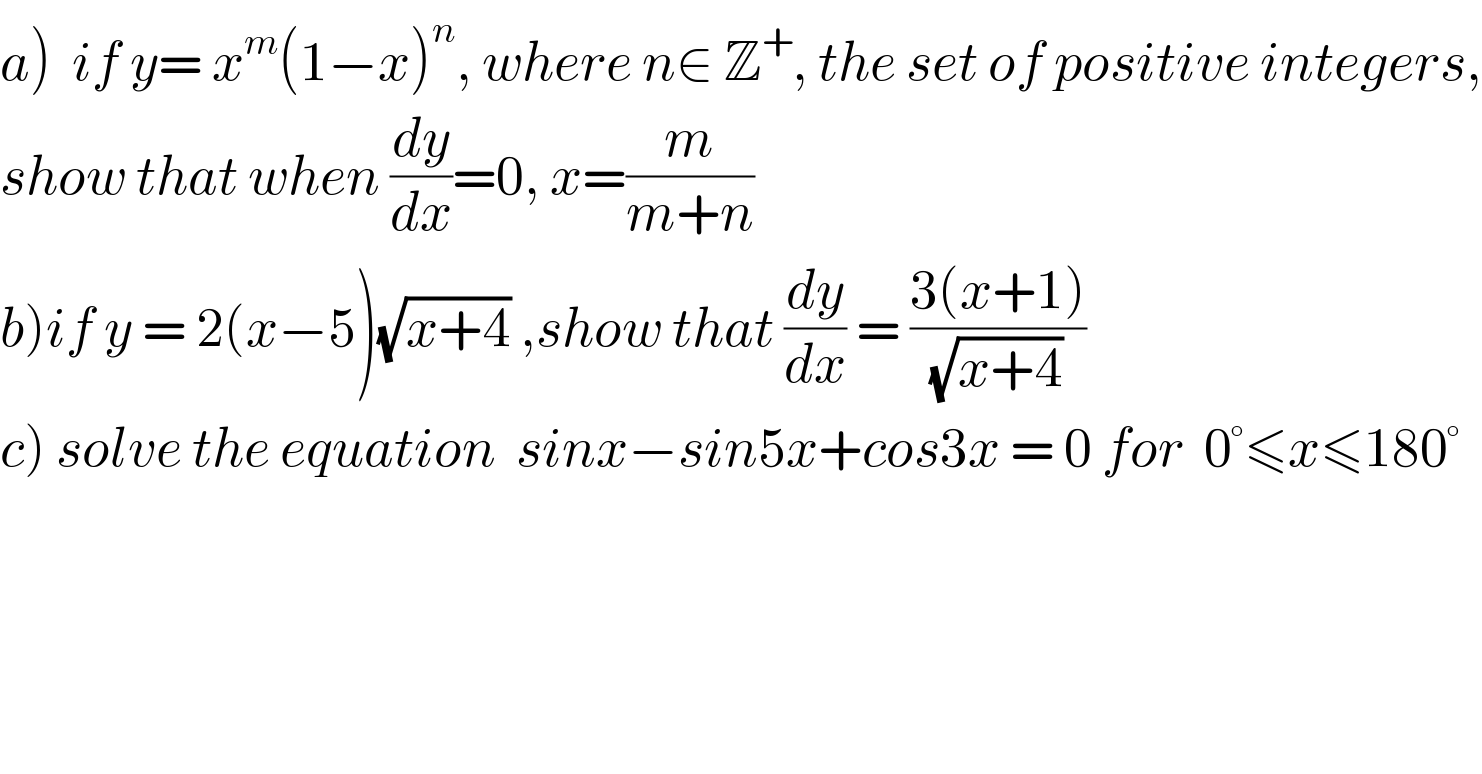
$$\left.{a}\right)\:\:{if}\:{y}=\:{x}^{{m}} \left(\mathrm{1}−{x}\right)^{{n}} ,\:{where}\:{n}\in\:\mathbb{Z}^{+} ,\:{the}\:{set}\:{of}\:{positive}\:{integers}, \\ $$$${show}\:{that}\:{when}\:\frac{{dy}}{{dx}}=\mathrm{0},\:{x}=\frac{{m}}{{m}+{n}} \\ $$$$\left.{b}\right){if}\:{y}\:=\:\mathrm{2}\left({x}−\mathrm{5}\right)\sqrt{{x}+\mathrm{4}}\:,{show}\:{that}\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{3}\left({x}+\mathrm{1}\right)}{\:\sqrt{{x}+\mathrm{4}}\:} \\ $$$$\left.{c}\right)\:{solve}\:{the}\:{equation}\:\:{sinx}−{sin}\mathrm{5}{x}+{cos}\mathrm{3}{x}\:=\:\mathrm{0}\:{for}\:\:\mathrm{0}°\leqslant{x}\leqslant\mathrm{180}° \\ $$
Commented by Prithwish sen last updated on 05/Jul/19
![a.(dy/dx) = mx^(m−1) (1−x)^n −nx^m (1−x)^(n−1) ⇒ x^(m−1) (1−x)^(n−1) [m(1−x)−nx] = 0 ⇒m(1−x) = nx ⇒ x = (m/(m+n)) b. (dy/dx) = 2(√(x+4)) +((2(x−5))/(2(√(x+4)))) = ((3(x+1))/( (√(x+4)))) c. −2cos3xsin2x+cos3x = 0 either cos3x=0 or sin2x = (1/2) ⇒ x= 30^° ⇒ x = 15^° please check.](https://www.tinkutara.com/question/Q63546.png)
$$\boldsymbol{\mathrm{a}}.\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{mx}^{\mathrm{m}−\mathrm{1}} \:\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}} −\mathrm{nx}^{\mathrm{m}} \:\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{x}^{\mathrm{m}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \:\left[\mathrm{m}\left(\mathrm{1}−\mathrm{x}\right)−\mathrm{nx}\right]\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{m}\left(\mathrm{1}−\mathrm{x}\right)\:=\:\mathrm{nx}\:\:\Rightarrow\:\mathrm{x}\:=\:\frac{\mathrm{m}}{\mathrm{m}+\mathrm{n}} \\ $$$$\boldsymbol{\mathrm{b}}.\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{2}\sqrt{\mathrm{x}+\mathrm{4}}\:+\frac{\mathrm{2}\left(\mathrm{x}−\mathrm{5}\right)}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{4}}}\:=\:\frac{\mathrm{3}\left(\mathrm{x}+\mathrm{1}\right)}{\:\sqrt{\mathrm{x}+\mathrm{4}}} \\ $$$$\boldsymbol{\mathrm{c}}.\:−\mathrm{2cos3xsin2x}+\mathrm{cos3x}\:=\:\mathrm{0} \\ $$$$\mathrm{either}\:\mathrm{cos3x}=\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{or}\:\mathrm{sin2x}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{x}=\:\mathrm{30}^{°} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{x}\:=\:\mathrm{15}^{°} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
