Menu Close

a-k-1-k-3-2-k-b-k-1-k-3-k-2-k-1-7-k-

Tinku Tara 0 Comments
Pin




Question Number 80142 by behi83417@gmail.com last updated on 31/Jan/20
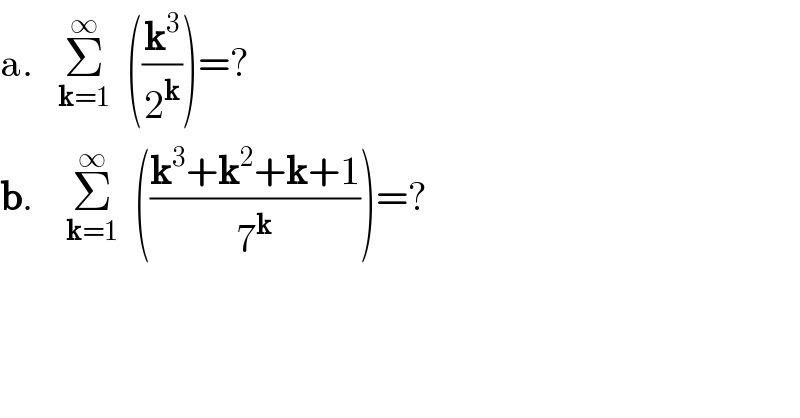
a. Σ_(k=1) ^∞ ((k^3 /2^k ))=? b. Σ_(k=1) ^∞ (((k^3 +k^2 +k+1)/7^k ))=?
$$\mathrm{a}.\:\:\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\left(\frac{\boldsymbol{\mathrm{k}}^{\mathrm{3}} }{\mathrm{2}^{\boldsymbol{\mathrm{k}}} }\right)=? \\ $$$$\boldsymbol{\mathrm{b}}.\:\:\:\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\left(\frac{\boldsymbol{\mathrm{k}}^{\mathrm{3}} +\boldsymbol{\mathrm{k}}^{\mathrm{2}} +\boldsymbol{\mathrm{k}}+\mathrm{1}}{\mathrm{7}^{\boldsymbol{\mathrm{k}}} }\right)=? \\ $$
Answered by mr W last updated on 31/Jan/20
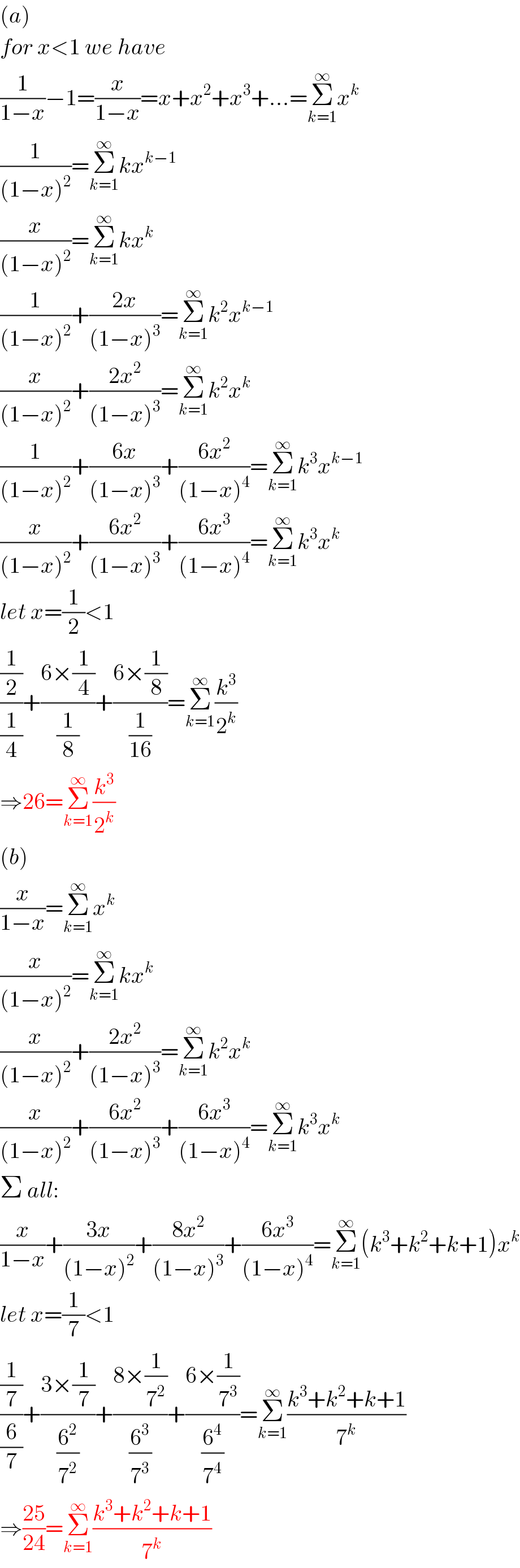
(a) for x<1 we have (1/(1−x))−1=(x/(1−x))=x+x^2 +x^3 +...=Σ_(k=1) ^∞ x^k (1/((1−x)^2 ))=Σ_(k=1) ^∞ kx^(k−1) (x/((1−x)^2 ))=Σ_(k=1) ^∞ kx^k (1/((1−x)^2 ))+((2x)/((1−x)^3 ))=Σ_(k=1) ^∞ k^2 x^(k−1) (x/((1−x)^2 ))+((2x^2 )/((1−x)^3 ))=Σ_(k=1) ^∞ k^2 x^k (1/((1−x)^2 ))+((6x)/((1−x)^3 ))+((6x^2 )/((1−x)^4 ))=Σ_(k=1) ^∞ k^3 x^(k−1) (x/((1−x)^2 ))+((6x^2 )/((1−x)^3 ))+((6x^3 )/((1−x)^4 ))=Σ_(k=1) ^∞ k^3 x^k let x=(1/2)<1 ((1/2)/(1/4))+((6×(1/4))/(1/8))+((6×(1/8))/(1/(16)))=Σ_(k=1) ^∞ (k^3 /2^k ) ⇒26=Σ_(k=1) ^∞ (k^3 /2^k ) (b) (x/(1−x))=Σ_(k=1) ^∞ x^k (x/((1−x)^2 ))=Σ_(k=1) ^∞ kx^k (x/((1−x)^2 ))+((2x^2 )/((1−x)^3 ))=Σ_(k=1) ^∞ k^2 x^k (x/((1−x)^2 ))+((6x^2 )/((1−x)^3 ))+((6x^3 )/((1−x)^4 ))=Σ_(k=1) ^∞ k^3 x^k Σ all: (x/(1−x))+((3x)/((1−x)^2 ))+((8x^2 )/((1−x)^3 ))+((6x^3 )/((1−x)^4 ))=Σ_(k=1) ^∞ (k^3 +k^2 +k+1)x^k let x=(1/7)<1 ((1/7)/(6/7))+((3×(1/7))/(6^2 /7^2 ))+((8×(1/7^2 ))/(6^3 /7^3 ))+((6×(1/7^3 ))/(6^4 /7^4 ))=Σ_(k=1) ^∞ ((k^3 +k^2 +k+1)/7^k ) ⇒((25)/(24))=Σ_(k=1) ^∞ ((k^3 +k^2 +k+1)/7^k )
$$\left({a}\right) \\ $$$${for}\:{x}<\mathrm{1}\:{we}\:{have} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{x}}−\mathrm{1}=\frac{{x}}{\mathrm{1}−{x}}={x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{k}} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{kx}^{{k}−\mathrm{1}} \\ $$$$\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{kx}^{{k}} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{k}^{\mathrm{2}} {x}^{{k}−\mathrm{1}} \\ $$$$\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{k}^{\mathrm{2}} {x}^{{k}} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{6}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{k}^{\mathrm{3}} {x}^{{k}−\mathrm{1}} \\ $$$$\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{6}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{k}^{\mathrm{3}} {x}^{{k}} \\ $$$${let}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{1} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{4}}}+\frac{\mathrm{6}×\frac{\mathrm{1}}{\mathrm{4}}}{\frac{\mathrm{1}}{\mathrm{8}}}+\frac{\mathrm{6}×\frac{\mathrm{1}}{\mathrm{8}}}{\frac{\mathrm{1}}{\mathrm{16}}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{3}} }{\mathrm{2}^{{k}} } \\ $$$$\Rightarrow\mathrm{26}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{3}} }{\mathrm{2}^{{k}} } \\ $$$$\left({b}\right) \\ $$$$\frac{{x}}{\mathrm{1}−{x}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{k}} \\ $$$$\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{kx}^{{k}} \\ $$$$\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{k}^{\mathrm{2}} {x}^{{k}} \\ $$$$\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{6}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{6}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{k}^{\mathrm{3}} {x}^{{k}} \\ $$$$\Sigma\:{all}: \\ $$$$\frac{{x}}{\mathrm{1}−{x}}+\frac{\mathrm{3}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{8}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{6}{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left({k}^{\mathrm{3}} +{k}^{\mathrm{2}} +{k}+\mathrm{1}\right){x}^{{k}} \\ $$$${let}\:{x}=\frac{\mathrm{1}}{\mathrm{7}}<\mathrm{1} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{7}}}{\frac{\mathrm{6}}{\mathrm{7}}}+\frac{\mathrm{3}×\frac{\mathrm{1}}{\mathrm{7}}}{\frac{\mathrm{6}^{\mathrm{2}} }{\mathrm{7}^{\mathrm{2}} }}+\frac{\mathrm{8}×\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }}{\frac{\mathrm{6}^{\mathrm{3}} }{\mathrm{7}^{\mathrm{3}} }}+\frac{\mathrm{6}×\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{3}} }}{\frac{\mathrm{6}^{\mathrm{4}} }{\mathrm{7}^{\mathrm{4}} }}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{3}} +{k}^{\mathrm{2}} +{k}+\mathrm{1}}{\mathrm{7}^{{k}} } \\ $$$$\Rightarrow\frac{\mathrm{25}}{\mathrm{24}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{\mathrm{3}} +{k}^{\mathrm{2}} +{k}+\mathrm{1}}{\mathrm{7}^{{k}} } \\ $$
Commented by behi83417@gmail.com last updated on 31/Jan/20
thank you very much dear master.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{master}. \\ $$
Answered by behi83417@gmail.com last updated on 31/Jan/20
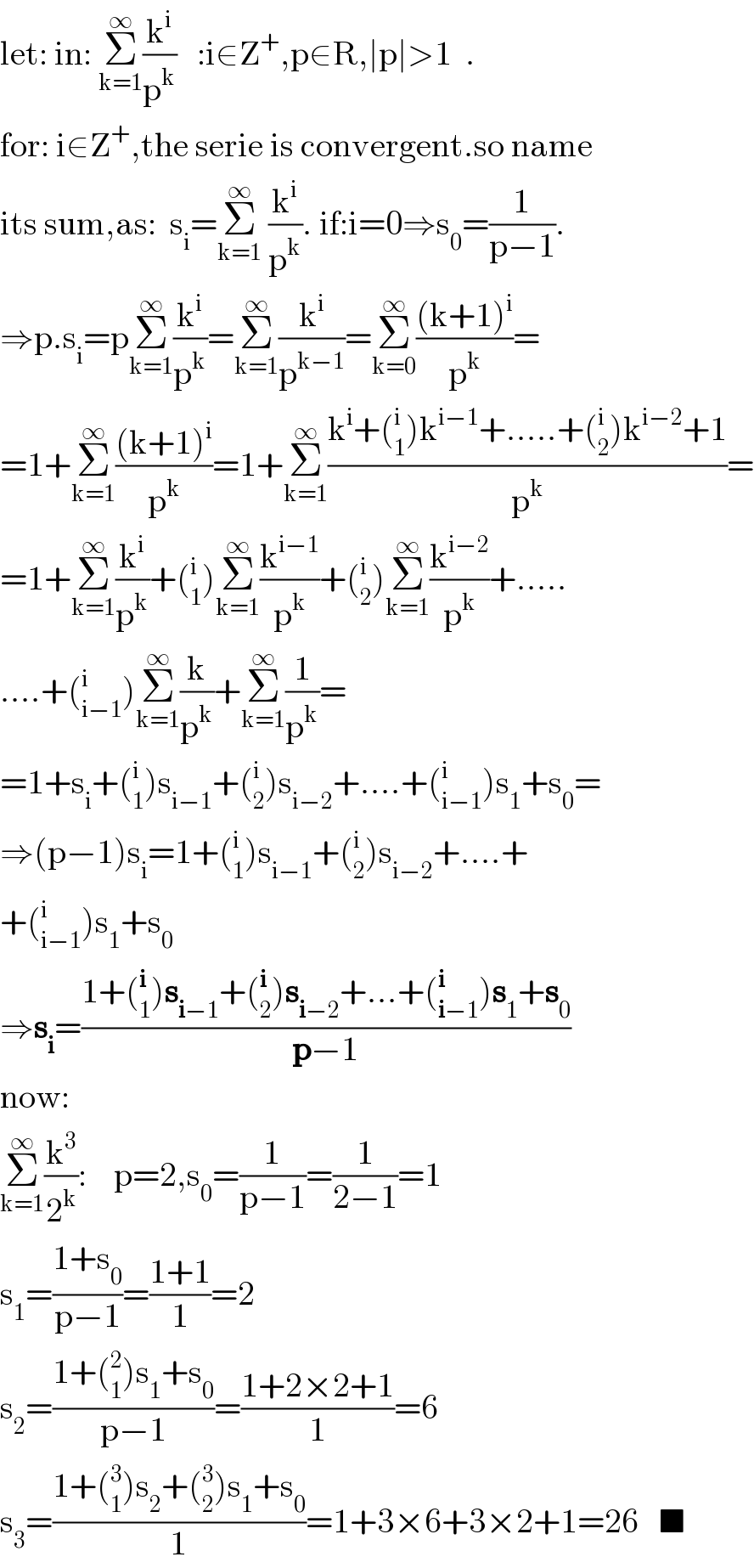
let: in: Σ_(k=1) ^∞ (k^i /p^k ) :i∈Z^+ ,p∈R,∣p∣>1 . for: i∈Z^+ ,the serie is convergent.so name its sum,as: s_i =Σ_(k=1) ^∞ (k^i /p^k ). if:i=0⇒s_0 =(1/(p−1)). ⇒p.s_i =pΣ_(k=1) ^∞ (k^i /p^k )=Σ_(k=1) ^∞ (k^i /p^(k−1) )=Σ_(k=0) ^∞ (((k+1)^i )/p^k )= =1+Σ_(k=1) ^∞ (((k+1)^i )/p^k )=1+Σ_(k=1) ^∞ ((k^i +(_1 ^i )k^(i−1) +.....+(_2 ^i )k^(i−2) +1)/p^k )= =1+Σ_(k=1) ^∞ (k^i /p^k )+(_1 ^i )Σ_(k=1) ^∞ (k^(i−1) /p^k )+(_2 ^i )Σ_(k=1) ^∞ (k^(i−2) /p^k )+..... ....+(_(i−1) ^i )Σ_(k=1) ^∞ (k/p^k )+Σ_(k=1) ^∞ (1/p^k )= =1+s_i +(_1 ^i )s_(i−1) +(_2 ^i )s_(i−2) +....+(_(i−1) ^i )s_1 +s_0 = ⇒(p−1)s_i =1+(_1 ^i )s_(i−1) +(_2 ^i )s_(i−2) +....+ +(_(i−1) ^i )s_1 +s_0 ⇒s_i =((1+(_1 ^i )s_(i−1) +(_2 ^i )s_(i−2) +...+(_(i−1) ^i )s_1 +s_0 )/(p−1)) now: Σ_(k=1) ^∞ (k^3 /2^k ): p=2,s_0 =(1/(p−1))=(1/(2−1))=1 s_1 =((1+s_0 )/(p−1))=((1+1)/1)=2 s_2 =((1+(_1 ^2 )s_1 +s_0 )/(p−1))=((1+2×2+1)/1)=6 s_3 =((1+(_1 ^3 )s_2 +(_2 ^3 )s_1 +s_0 )/1)=1+3×6+3×2+1=26 ■
$$\mathrm{let}:\:\mathrm{in}:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}^{\mathrm{i}} }{\mathrm{p}^{\mathrm{k}} }\:\:\::\mathrm{i}\in\mathrm{Z}^{+} ,\mathrm{p}\in\mathrm{R},\mid\mathrm{p}\mid>\mathrm{1}\:\:. \\ $$$$\mathrm{for}:\:\mathrm{i}\in\mathrm{Z}^{+} ,\mathrm{the}\:\mathrm{serie}\:\mathrm{is}\:\mathrm{convergent}.\mathrm{so}\:\mathrm{name} \\ $$$$\mathrm{its}\:\mathrm{sum},\mathrm{as}:\:\:\mathrm{s}_{\mathrm{i}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{k}^{\mathrm{i}} }{\mathrm{p}^{\mathrm{k}} }.\:\mathrm{if}:\mathrm{i}=\mathrm{0}\Rightarrow\mathrm{s}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{p}−\mathrm{1}}. \\ $$$$\Rightarrow\mathrm{p}.\mathrm{s}_{\mathrm{i}} =\mathrm{p}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}^{\mathrm{i}} }{\mathrm{p}^{\mathrm{k}} }=\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}^{\mathrm{i}} }{\mathrm{p}^{\mathrm{k}−\mathrm{1}} }=\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{p}^{\mathrm{k}} }= \\ $$$$=\mathrm{1}+\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{p}^{\mathrm{k}} }=\mathrm{1}+\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}^{\mathrm{i}} +\left(_{\mathrm{1}} ^{\mathrm{i}} \right)\mathrm{k}^{\mathrm{i}−\mathrm{1}} +…..+\left(_{\mathrm{2}} ^{\mathrm{i}} \right)\mathrm{k}^{\mathrm{i}−\mathrm{2}} +\mathrm{1}}{\mathrm{p}^{\mathrm{k}} }= \\ $$$$=\mathrm{1}+\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}^{\mathrm{i}} }{\mathrm{p}^{\mathrm{k}} }+\left(_{\mathrm{1}} ^{\mathrm{i}} \right)\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}^{\mathrm{i}−\mathrm{1}} }{\mathrm{p}^{\mathrm{k}} }+\left(_{\mathrm{2}} ^{\mathrm{i}} \right)\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}^{\mathrm{i}−\mathrm{2}} }{\mathrm{p}^{\mathrm{k}} }+….. \\ $$$$….+\left(_{\mathrm{i}−\mathrm{1}} ^{\mathrm{i}} \right)\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}}{\mathrm{p}^{\mathrm{k}} }+\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{p}^{\mathrm{k}} }= \\ $$$$=\mathrm{1}+\mathrm{s}_{\mathrm{i}} +\left(_{\mathrm{1}} ^{\mathrm{i}} \right)\mathrm{s}_{\mathrm{i}−\mathrm{1}} +\left(_{\mathrm{2}} ^{\mathrm{i}} \right)\mathrm{s}_{\mathrm{i}−\mathrm{2}} +….+\left(_{\mathrm{i}−\mathrm{1}} ^{\mathrm{i}} \right)\mathrm{s}_{\mathrm{1}} +\mathrm{s}_{\mathrm{0}} = \\ $$$$\Rightarrow\left(\mathrm{p}−\mathrm{1}\right)\mathrm{s}_{\mathrm{i}} =\mathrm{1}+\left(_{\mathrm{1}} ^{\mathrm{i}} \right)\mathrm{s}_{\mathrm{i}−\mathrm{1}} +\left(_{\mathrm{2}} ^{\mathrm{i}} \right)\mathrm{s}_{\mathrm{i}−\mathrm{2}} +….+ \\ $$$$+\left(_{\mathrm{i}−\mathrm{1}} ^{\mathrm{i}} \right)\mathrm{s}_{\mathrm{1}} +\mathrm{s}_{\mathrm{0}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{s}}_{\boldsymbol{\mathrm{i}}} =\frac{\mathrm{1}+\left(_{\mathrm{1}} ^{\boldsymbol{\mathrm{i}}} \right)\boldsymbol{\mathrm{s}}_{\boldsymbol{\mathrm{i}}−\mathrm{1}} +\left(_{\mathrm{2}} ^{\boldsymbol{\mathrm{i}}} \right)\boldsymbol{\mathrm{s}}_{\boldsymbol{\mathrm{i}}−\mathrm{2}} +…+\left(_{\boldsymbol{\mathrm{i}}−\mathrm{1}} ^{\boldsymbol{\mathrm{i}}} \right)\boldsymbol{\mathrm{s}}_{\mathrm{1}} +\boldsymbol{\mathrm{s}}_{\mathrm{0}} }{\boldsymbol{\mathrm{p}}−\mathrm{1}} \\ $$$$\mathrm{now}: \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{k}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{k}} }:\:\:\:\:\mathrm{p}=\mathrm{2},\mathrm{s}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{p}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}−\mathrm{1}}=\mathrm{1} \\ $$$$\mathrm{s}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{s}_{\mathrm{0}} }{\mathrm{p}−\mathrm{1}}=\frac{\mathrm{1}+\mathrm{1}}{\mathrm{1}}=\mathrm{2} \\ $$$$\mathrm{s}_{\mathrm{2}} =\frac{\mathrm{1}+\left(_{\mathrm{1}} ^{\mathrm{2}} \right)\mathrm{s}_{\mathrm{1}} +\mathrm{s}_{\mathrm{0}} }{\mathrm{p}−\mathrm{1}}=\frac{\mathrm{1}+\mathrm{2}×\mathrm{2}+\mathrm{1}}{\mathrm{1}}=\mathrm{6} \\ $$$$\mathrm{s}_{\mathrm{3}} =\frac{\mathrm{1}+\left(_{\mathrm{1}} ^{\mathrm{3}} \right)\mathrm{s}_{\mathrm{2}} +\left(_{\mathrm{2}} ^{\mathrm{3}} \right)\mathrm{s}_{\mathrm{1}} +\mathrm{s}_{\mathrm{0}} }{\mathrm{1}}=\mathrm{1}+\mathrm{3}×\mathrm{6}+\mathrm{3}×\mathrm{2}+\mathrm{1}=\mathrm{26}\:\:\:\blacksquare \\ $$
Commented by mr W last updated on 01/Feb/20
method for general case, very nice sir!
$${method}\:{for}\:{general}\:{case},\:{very}\:{nice}\:{sir}! \\ $$
Commented by behi83417@gmail.com last updated on 01/Feb/20
thank you for time sir.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *