Question Number 51617 by Saorey last updated on 29/Dec/18

$$\mathrm{A}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −{e}^{−{x}} −\mathrm{2}{x}}{{x}^{\mathrm{3}} }\left({without}\:\right. \\ $$$$\left.{using}\:{L}'\mathrm{hopital}\:\mathrm{rule}\right) \\ $$$$ \\ $$
Commented by aseerimad last updated on 29/Dec/18
how to do it by L'hopital ?
Commented by tanmay.chaudhury50@gmail.com last updated on 29/Dec/18
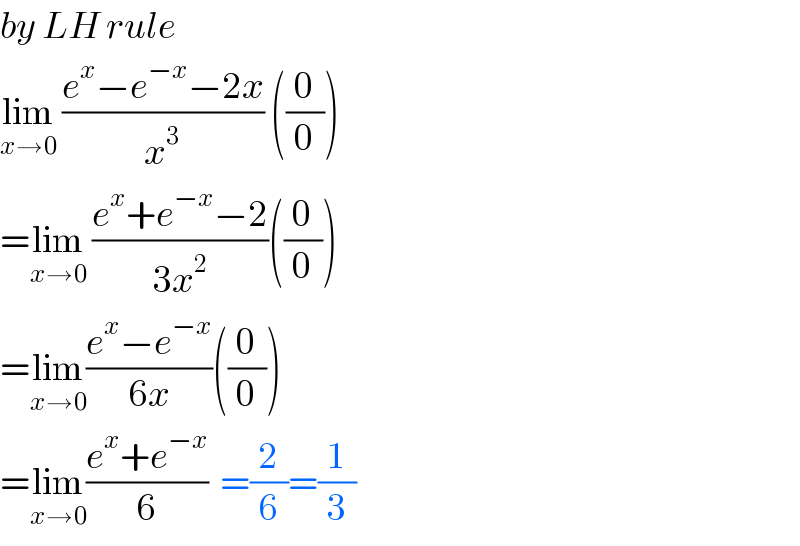
$${by}\:{LH}\:{rule} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} −{e}^{−{x}} −\mathrm{2}{x}}{{x}^{\mathrm{3}} }\:\left(\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} +{e}^{−{x}} −\mathrm{2}}{\mathrm{3}{x}^{\mathrm{2}} }\left(\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{6}{x}}\left(\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{6}}\:\:=\frac{\mathrm{2}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by Smail last updated on 29/Dec/18
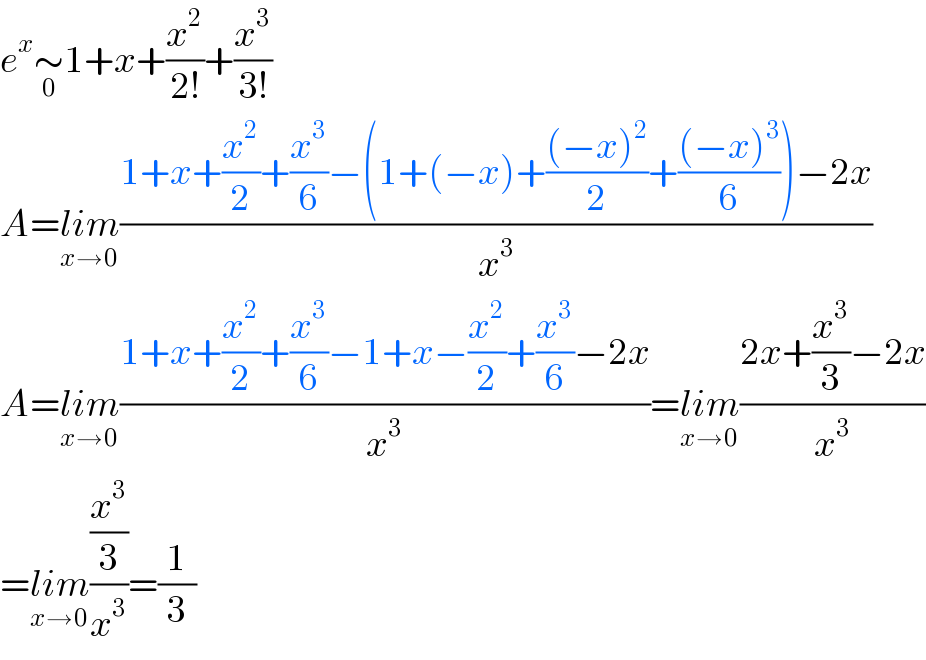
$${e}^{{x}} \underset{\mathrm{0}} {\sim}\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!} \\ $$$${A}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−\left(\mathrm{1}+\left(−{x}\right)+\frac{\left(−{x}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(−{x}\right)^{\mathrm{3}} }{\mathrm{6}}\right)−\mathrm{2}{x}}{{x}^{\mathrm{3}} } \\ $$$${A}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−\mathrm{1}+{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−\mathrm{2}{x}}{{x}^{\mathrm{3}} }=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{2}{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}{x}}{{x}^{\mathrm{3}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
