Menu Close

a-lim-x-1-1-2-1-x-1-3-1-x-1-3-b-lim-x-ln-x-1-x-2-ln-x-x-2-1-ln-x-1-x-1-2-

Tinku Tara 0 Comments
Pin




Question Number 117551 by bobhans last updated on 12/Oct/20
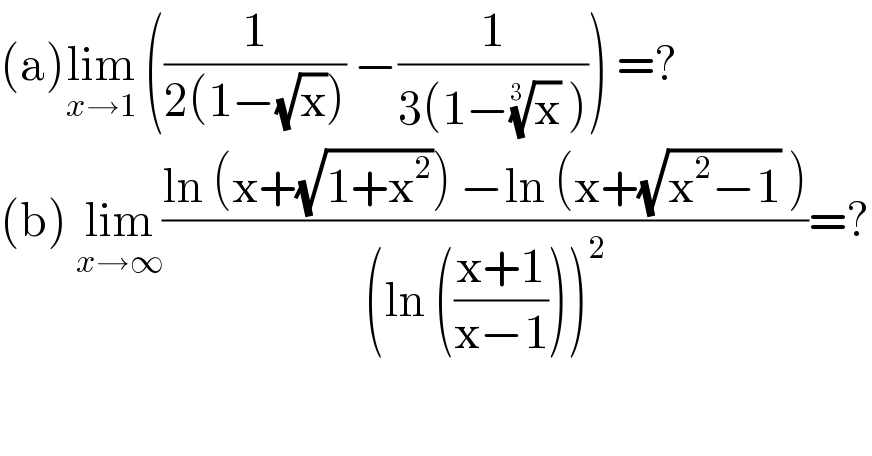
(a)lim_(x→1) ((1/(2(1−(√x)))) −(1/(3(1−(x)^(1/(3 )) )))) =? (b) lim_(x→∞) ((ln (x+(√(1+x^2 ))) −ln (x+(√(x^2 −1)) ))/((ln (((x+1)/(x−1))))^2 ))=?
$$\left(\mathrm{a}\right)\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{x}}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\sqrt[{\mathrm{3}\:}]{\mathrm{x}}\:\right)}\right)\:=? \\ $$$$\left(\mathrm{b}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:−\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\right)}{\left(\mathrm{ln}\:\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)\right)^{\mathrm{2}} }=? \\ $$
Answered by bemath last updated on 13/Oct/20
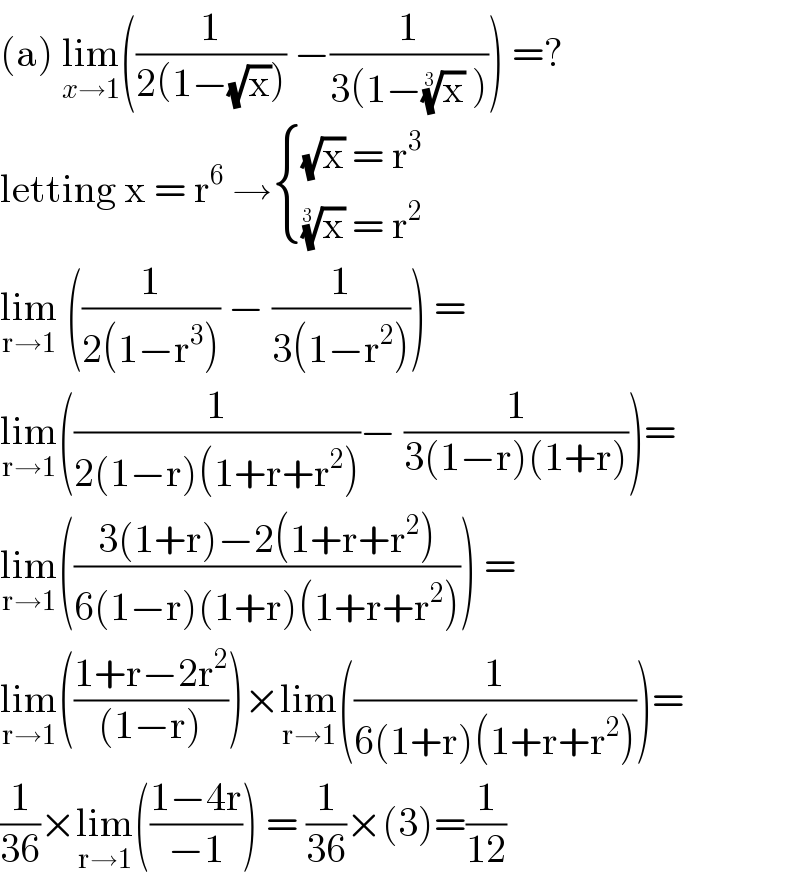
(a) lim_(x→1) ((1/(2(1−(√x)))) −(1/(3(1−(x)^(1/3) )))) =? letting x = r^6 → { (((√x) = r^3 )),(((x)^(1/(3 )) = r^2 )) :} lim_(r→1) ((1/(2(1−r^3 ))) − (1/(3(1−r^2 )))) = lim_(r→1) ((1/(2(1−r)(1+r+r^2 )))− (1/(3(1−r)(1+r))))= lim_(r→1) (((3(1+r)−2(1+r+r^2 ))/(6(1−r)(1+r)(1+r+r^2 )))) = lim_(r→1) (((1+r−2r^2 )/((1−r))))×lim_(r→1) ((1/(6(1+r)(1+r+r^2 ))))= (1/(36))×lim_(r→1) (((1−4r)/(−1))) = (1/(36))×(3)=(1/(12))
$$\left(\mathrm{a}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{x}}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\sqrt[{\mathrm{3}}]{\mathrm{x}}\:\right)}\right)\:=? \\ $$$$\mathrm{letting}\:\mathrm{x}\:=\:\mathrm{r}^{\mathrm{6}} \:\rightarrow\begin{cases}{\sqrt{\mathrm{x}}\:=\:\mathrm{r}^{\mathrm{3}} }\\{\sqrt[{\mathrm{3}\:}]{\mathrm{x}}\:=\:\mathrm{r}^{\mathrm{2}} }\end{cases} \\ $$$$\underset{\mathrm{r}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{r}^{\mathrm{3}} \right)}\:−\:\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\mathrm{r}^{\mathrm{2}} \right)}\right)\:= \\ $$$$\underset{\mathrm{r}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\mathrm{r}\right)\left(\mathrm{1}+\mathrm{r}+\mathrm{r}^{\mathrm{2}} \right)}−\:\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\mathrm{r}\right)\left(\mathrm{1}+\mathrm{r}\right)}\right)= \\ $$$$\underset{\mathrm{r}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{3}\left(\mathrm{1}+\mathrm{r}\right)−\mathrm{2}\left(\mathrm{1}+\mathrm{r}+\mathrm{r}^{\mathrm{2}} \right)}{\mathrm{6}\left(\mathrm{1}−\mathrm{r}\right)\left(\mathrm{1}+\mathrm{r}\right)\left(\mathrm{1}+\mathrm{r}+\mathrm{r}^{\mathrm{2}} \right)}\right)\:= \\ $$$$\underset{\mathrm{r}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}+\mathrm{r}−\mathrm{2r}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{r}\right)}\right)×\underset{\mathrm{r}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{1}+\mathrm{r}\right)\left(\mathrm{1}+\mathrm{r}+\mathrm{r}^{\mathrm{2}} \right)}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{36}}×\underset{\mathrm{r}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}−\mathrm{4r}}{−\mathrm{1}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{36}}×\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Answered by TANMAY PANACEA last updated on 12/Oct/20
a) t^6 =x lim_(t→1) ((1/(2(1−t^3 )))−(1/(3(1−t^2 )))) lim_(t→1) [(1/(2(1−t)(1+t+t^2 )))−(1/(3(1+t)(1−t)))] =lim_(t→1) [((3(1+t)−2(1+t+t^2 ))/(6(1−t)(1+t+t^2 )(1+t)))] =lim_(t→1) [((3+3t−2−2t−2t^2 )/(6(1−t)(1+t+t^2 )(1+t)))] =lim_(t→1) [((1+t−2t^2 )/(6(1−t)(1+t+t^2 )(1+t)))] =lim_(t→1) [(((1+2t)(1−t))/(6(1−t)(1+t+t^2 )(1+t)))]=(3/(6×3×2))=(1/(12))
$$\left.{a}\right)\:{t}^{\mathrm{6}} ={x} \\ $$$$\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\:\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{3}} \right)}−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}\right) \\ $$$$\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left[\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−{t}\right)}\right] \\ $$$$=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{3}\left(\mathrm{1}+{t}\right)−\mathrm{2}\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right)}{\mathrm{6}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}\right)}\right] \\ $$$$=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left[\frac{\mathrm{3}+\mathrm{3}{t}−\mathrm{2}−\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{6}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}\right)}\right] \\ $$$$=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left[\frac{\mathrm{1}+{t}−\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{6}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}\right)}\right] \\ $$$$=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\frac{\left(\mathrm{1}+\mathrm{2}{t}\right)\left(\mathrm{1}−{t}\right)}{\mathrm{6}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}\right)}\right]=\frac{\mathrm{3}}{\mathrm{6}×\mathrm{3}×\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Commented by TANMAY PANACEA last updated on 12/Oct/20
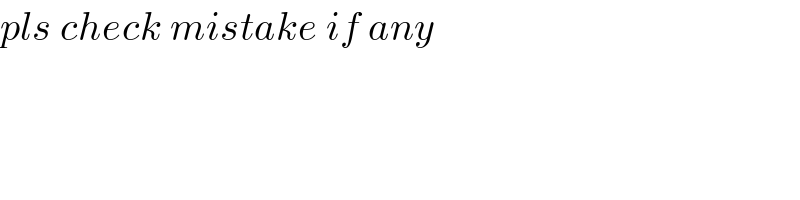
pls check mistake if any
$${pls}\:{check}\:{mistake}\:{if}\:{any} \\ $$
Answered by TANMAY PANACEA last updated on 12/Oct/20
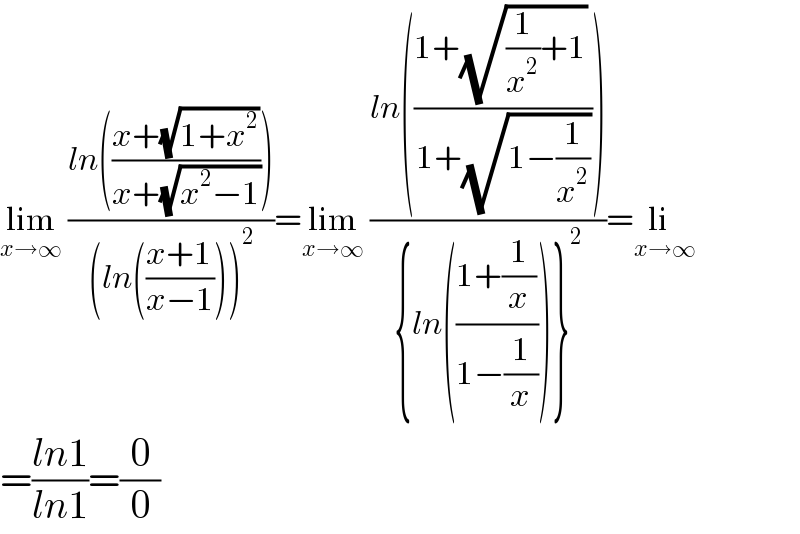
lim_(x→∞) ((ln(((x+(√(1+x^2 )))/(x+(√(x^2 −1))))))/((ln(((x+1)/(x−1))))^2 ))=lim_(x→∞) ((ln(((1+(√((1/x^2 )+1)) )/(1+(√(1−(1/x^2 )))))))/({ln(((1+(1/x))/(1−(1/x))))}^2 ))=li_(x→∞) =((ln1)/(ln1))=(0/0)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{ln}\left(\frac{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\right)}{\left({ln}\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)\right)^{\mathrm{2}} }=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{ln}\left(\frac{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}\:}{\mathrm{1}+\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}\right)}{\left\{{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}}}{\mathrm{1}−\frac{\mathrm{1}}{{x}}}\right)\right\}^{\mathrm{2}} }=\underset{{x}\rightarrow\infty} {\mathrm{li}} \\ $$$$=\frac{{ln}\mathrm{1}}{{ln}\mathrm{1}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$
Commented by MJS_new last updated on 12/Oct/20
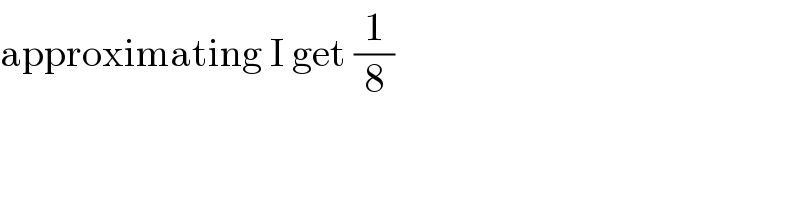
approximating I get (1/8)
$$\mathrm{approximating}\:\mathrm{I}\:\mathrm{get}\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *