Menu Close

a-lim-x-pi-4-cos-x-sin-x-3-2-2-1-sin-2x-b-lim-x-0-sin-x-1-x-

Tinku Tara 0 Comments
Pin




Question Number 34540 by rahul 19 last updated on 07/May/18
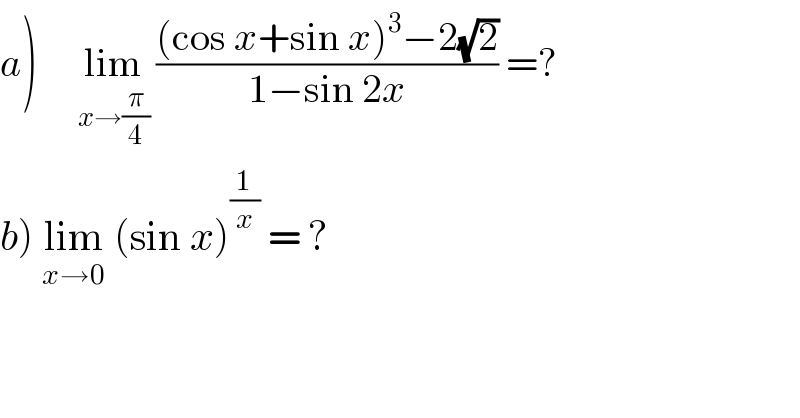
a) lim_(x→(π/4)) (((cos x+sin x)^3 −2(√2))/(1−sin 2x)) =? b) lim_(x→0) (sin x)^(1/x) = ?
$$\left.{a}\right)\:\:\:\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)^{\mathrm{3}} −\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}}\:=? \\ $$$$\left.{b}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{sin}\:{x}\right)^{\frac{\mathrm{1}}{{x}}} \:=\:? \\ $$
Commented by abdo mathsup 649 cc last updated on 07/May/18
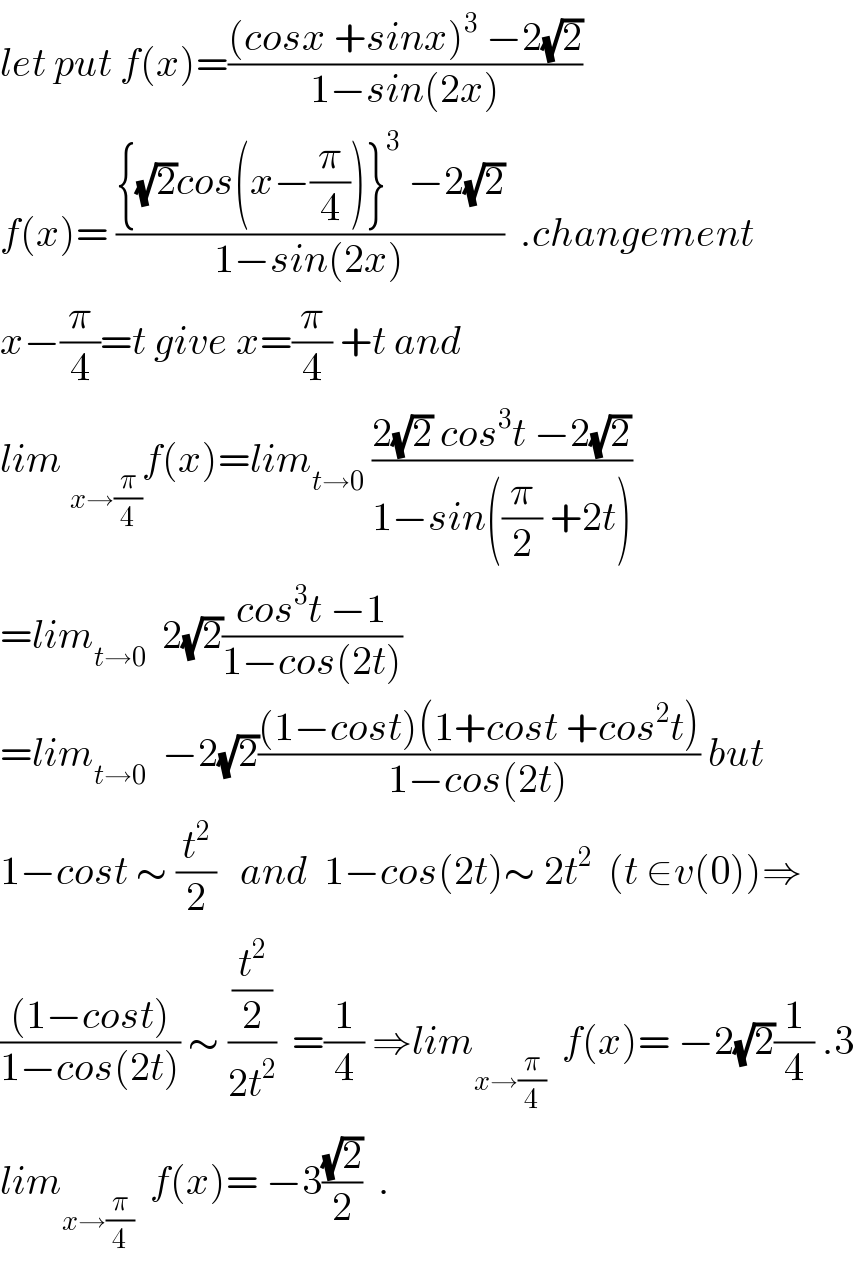
let put f(x)=(((cosx +sinx)^3 −2(√2))/(1−sin(2x))) f(x)= (({(√2)cos(x−(π/4))}^3 −2(√2))/(1−sin(2x))) .changement x−(π/4)=t give x=(π/4) +t and lim _(x→(π/4)) f(x)=lim_(t→0) ((2(√2) cos^3 t −2(√2))/(1−sin((π/2) +2t))) =lim_(t→0) 2(√2)((cos^3 t −1)/(1−cos(2t))) =lim_(t→0) −2(√2)(((1−cost)(1+cost +cos^2 t))/(1−cos(2t))) but 1−cost ∼ (t^2 /2) and 1−cos(2t)∼ 2t^2 (t ∈v(0))⇒ (((1−cost))/(1−cos(2t))) ∼ ((t^2 /2)/(2t^2 )) =(1/4) ⇒lim_(x→(π/4)) f(x)= −2(√2)(1/4) .3 lim_(x→(π/4)) f(x)= −3((√2)/2) .
$${let}\:{put}\:{f}\left({x}\right)=\frac{\left({cosx}\:+{sinx}\right)^{\mathrm{3}} \:−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}−{sin}\left(\mathrm{2}{x}\right)} \\ $$$${f}\left({x}\right)=\:\frac{\left\{\sqrt{\mathrm{2}}{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\right\}^{\mathrm{3}} \:−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}−{sin}\left(\mathrm{2}{x}\right)}\:\:.{changement} \\ $$$${x}−\frac{\pi}{\mathrm{4}}={t}\:{give}\:{x}=\frac{\pi}{\mathrm{4}}\:+{t}\:{and} \\ $$$${lim}\:_{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {f}\left({x}\right)={lim}_{{t}\rightarrow\mathrm{0}} \:\frac{\mathrm{2}\sqrt{\mathrm{2}}\:{cos}^{\mathrm{3}} {t}\:−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}−{sin}\left(\frac{\pi}{\mathrm{2}}\:+\mathrm{2}{t}\right)} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\mathrm{2}\sqrt{\mathrm{2}}\frac{{cos}^{\mathrm{3}} {t}\:−\mathrm{1}}{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:−\mathrm{2}\sqrt{\mathrm{2}}\frac{\left(\mathrm{1}−{cost}\right)\left(\mathrm{1}+{cost}\:+{cos}^{\mathrm{2}} {t}\right)}{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}\:{but} \\ $$$$\mathrm{1}−{cost}\:\sim\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\:\:{and}\:\:\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)\sim\:\mathrm{2}{t}^{\mathrm{2}} \:\:\left({t}\:\in{v}\left(\mathrm{0}\right)\right)\Rightarrow \\ $$$$\frac{\left(\mathrm{1}−{cost}\right)}{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}\:\sim\:\frac{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{2}{t}^{\mathrm{2}} }\:\:=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{lim}_{{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\:{f}\left({x}\right)=\:−\mathrm{2}\sqrt{\mathrm{2}}\frac{\mathrm{1}}{\mathrm{4}}\:.\mathrm{3} \\ $$$${lim}_{{x}\rightarrow\frac{\pi}{\mathrm{4}}} \:\:{f}\left({x}\right)=\:−\mathrm{3}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:. \\ $$
Commented by abdo mathsup 649 cc last updated on 08/May/18
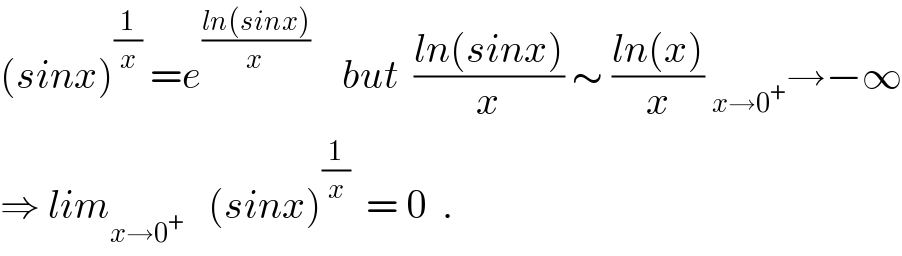
(sinx)^(1/x) =e^((ln(sinx))/(x )) but ((ln(sinx))/x) ∼ ((ln(x))/x) _(x→0^+ ) →−∞ ⇒ lim_(x→0^+ ) (sinx)^(1/x) = 0 .
$$\left({sinx}\right)^{\frac{\mathrm{1}}{{x}}} \:={e}^{\frac{{ln}\left({sinx}\right)}{{x}\:}} \:\:\:\:{but}\:\:\frac{{ln}\left({sinx}\right)}{{x}}\:\sim\:\frac{{ln}\left({x}\right)}{{x}}\:_{{x}\rightarrow\mathrm{0}^{+} } \rightarrow−\infty \\ $$$$\Rightarrow\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:\left({sinx}\right)^{\frac{\mathrm{1}}{{x}}} \:\:=\:\mathrm{0}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *