Question Number 183965 by nadovic last updated on 01/Jan/23

$$\mathrm{A}\:\mathrm{linear}\:\mathrm{transformation}\:\boldsymbol{{E}},\:\mathrm{of}\:\mathrm{the} \\ $$$${x}−{y}\:\mathrm{plane}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{as} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{E}}:\left({x},\:{y}\right)\:\rightarrow\:\left(\mathrm{2}{x}+{y},\:\mathrm{2}{x}+\mathrm{3}{y}\right) \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{that} \\ $$$$\mathrm{remains}\:\mathrm{invariant}\:\mathrm{under}\:\mathrm{the} \\ $$$$\mathrm{transformation}. \\ $$
Answered by mr W last updated on 01/Jan/23
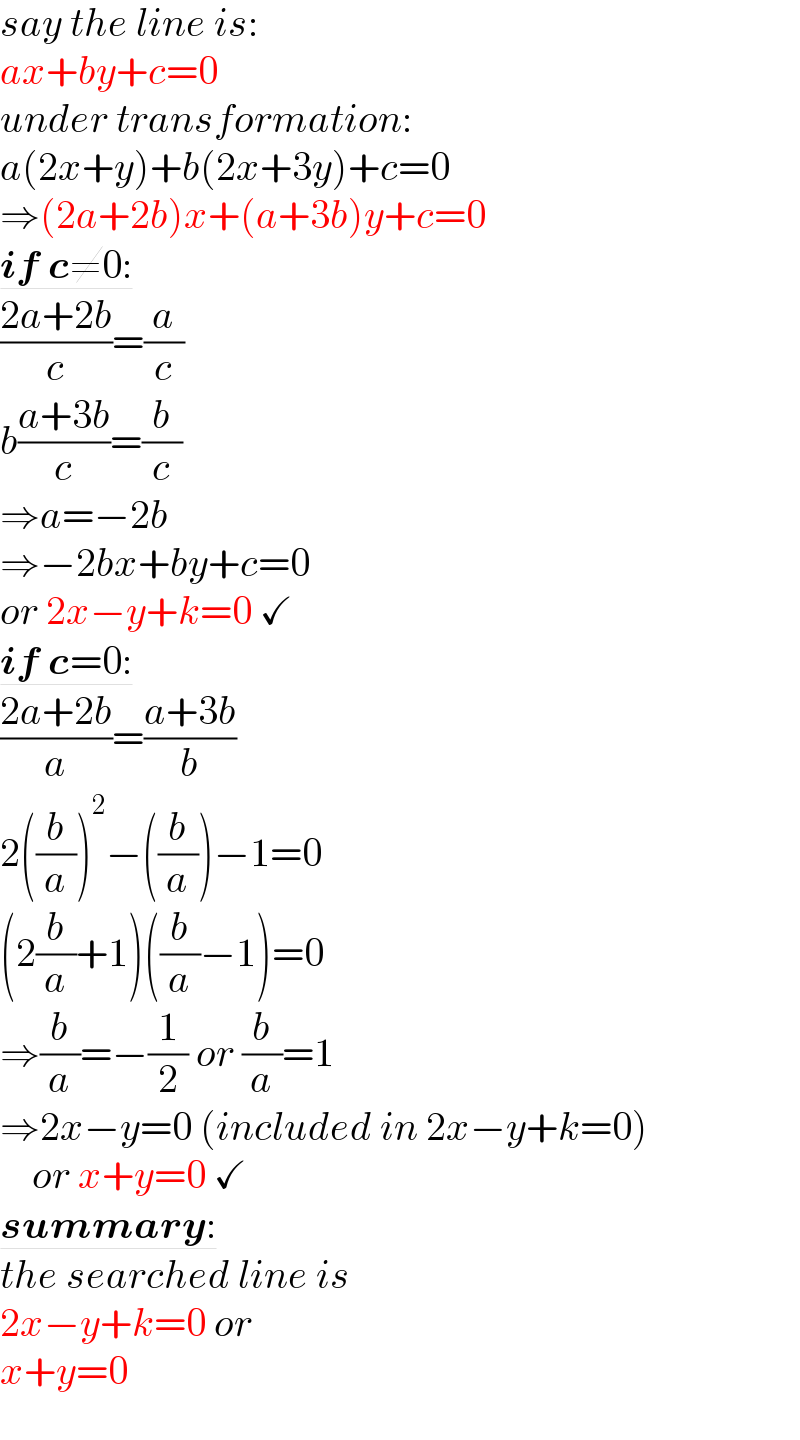
$${say}\:{the}\:{line}\:{is}: \\ $$$${ax}+{by}+{c}=\mathrm{0} \\ $$$${under}\:{transformation}: \\ $$$${a}\left(\mathrm{2}{x}+{y}\right)+{b}\left(\mathrm{2}{x}+\mathrm{3}{y}\right)+{c}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{a}+\mathrm{2}{b}\right){x}+\left({a}+\mathrm{3}{b}\right){y}+{c}=\mathrm{0} \\ $$$$\underline{\boldsymbol{{if}}\:\boldsymbol{{c}}\neq\mathrm{0}:} \\ $$$$\frac{\mathrm{2}{a}+\mathrm{2}{b}}{{c}}=\frac{{a}}{{c}} \\ $$$${b}\frac{{a}+\mathrm{3}{b}}{{c}}=\frac{{b}}{{c}} \\ $$$$\Rightarrow{a}=−\mathrm{2}{b} \\ $$$$\Rightarrow−\mathrm{2}{bx}+{by}+{c}=\mathrm{0} \\ $$$${or}\:\mathrm{2}{x}−{y}+{k}=\mathrm{0}\:\checkmark \\ $$$$\underline{\boldsymbol{{if}}\:\boldsymbol{{c}}=\mathrm{0}:} \\ $$$$\frac{\mathrm{2}{a}+\mathrm{2}{b}}{{a}}=\frac{{a}+\mathrm{3}{b}}{{b}} \\ $$$$\mathrm{2}\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} −\left(\frac{{b}}{{a}}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}\frac{{b}}{{a}}+\mathrm{1}\right)\left(\frac{{b}}{{a}}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\frac{{b}}{{a}}=−\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:\frac{{b}}{{a}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{x}−{y}=\mathrm{0}\:\left({included}\:{in}\:\mathrm{2}{x}−{y}+{k}=\mathrm{0}\right)\: \\ $$$$\:\:\:\:{or}\:{x}+{y}=\mathrm{0}\:\checkmark \\ $$$$\underline{\boldsymbol{{summary}}:} \\ $$$${the}\:{searched}\:{line}\:{is} \\ $$$$\mathrm{2}{x}−{y}+{k}=\mathrm{0}\:{or} \\ $$$${x}+{y}=\mathrm{0} \\ $$
Commented by nadovic last updated on 01/Jan/23
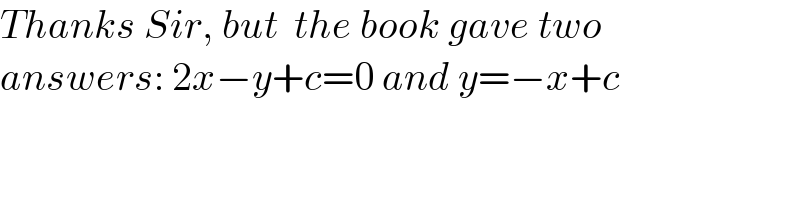
$${Thanks}\:{Sir},\:{but}\:\:{the}\:{book}\:{gave}\:{two} \\ $$$${answers}:\:\mathrm{2}{x}−{y}+{c}=\mathrm{0}\:{and}\:{y}=−{x}+{c} \\ $$
Commented by mr W last updated on 01/Jan/23
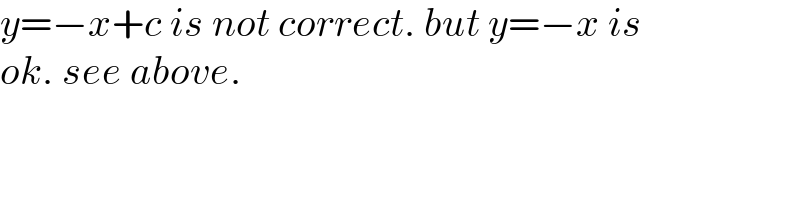
$${y}=−{x}+{c}\:{is}\:{not}\:{correct}.\:{but}\:{y}=−{x}\:{is} \\ $$$${ok}.\:{see}\:{above}. \\ $$
Commented by nadovic last updated on 01/Jan/23
$$\mathrm{Alright}..\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}. \\ $$
