Question Number 162960 by mnjuly1970 last updated on 02/Jan/22
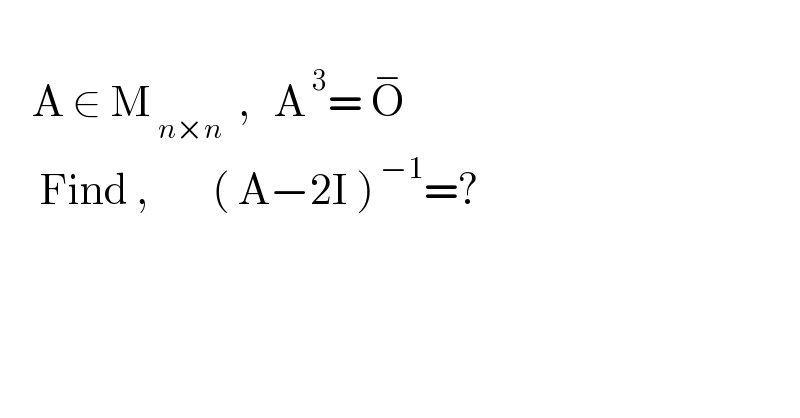
$$ \\ $$$$\:\:\:\:\mathrm{A}\:\in\:\mathrm{M}_{\:{n}×{n}} \:\:,\:\:\:\mathrm{A}^{\:\mathrm{3}} =\:\overset{−} {\mathrm{O}}\:\: \\ $$$$\:\:\:\:\:\mathrm{Find}\:,\:\:\:\:\:\:\:\:\left(\:\mathrm{A}−\mathrm{2I}\:\right)^{\:−\mathrm{1}} =? \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 03/Jan/22
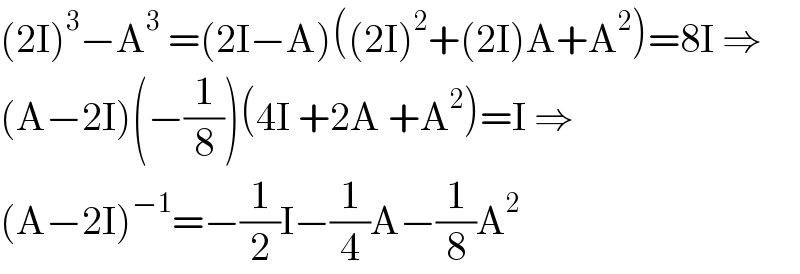
$$\left(\mathrm{2I}\right)^{\mathrm{3}} −\mathrm{A}^{\mathrm{3}} \:=\left(\mathrm{2I}−\mathrm{A}\right)\left(\left(\mathrm{2I}\right)^{\mathrm{2}} +\left(\mathrm{2I}\right)\mathrm{A}+\mathrm{A}^{\mathrm{2}} \right)=\mathrm{8I}\:\Rightarrow \\ $$$$\left(\mathrm{A}−\mathrm{2I}\right)\left(−\frac{\mathrm{1}}{\mathrm{8}}\right)\left(\mathrm{4I}\:+\mathrm{2A}\:+\mathrm{A}^{\mathrm{2}} \right)=\mathrm{I}\:\Rightarrow \\ $$$$\left(\mathrm{A}−\mathrm{2I}\right)^{−\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{A}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{A}^{\mathrm{2}} \\ $$
