Menu Close

A-man-and-a-woman-have-3-boys-and-3-girls-i-in-how-many-ways-will-they-sit-in-a-row-such-that-the-3-boys-and-3-girls-are-inbetween-the-man-and-woman-ii-Say-the-man-decides-of-the-3-boys-and-

Tinku Tara 0 Comments
Pin




Question Number 99175 by Rio Michael last updated on 19/Jun/20
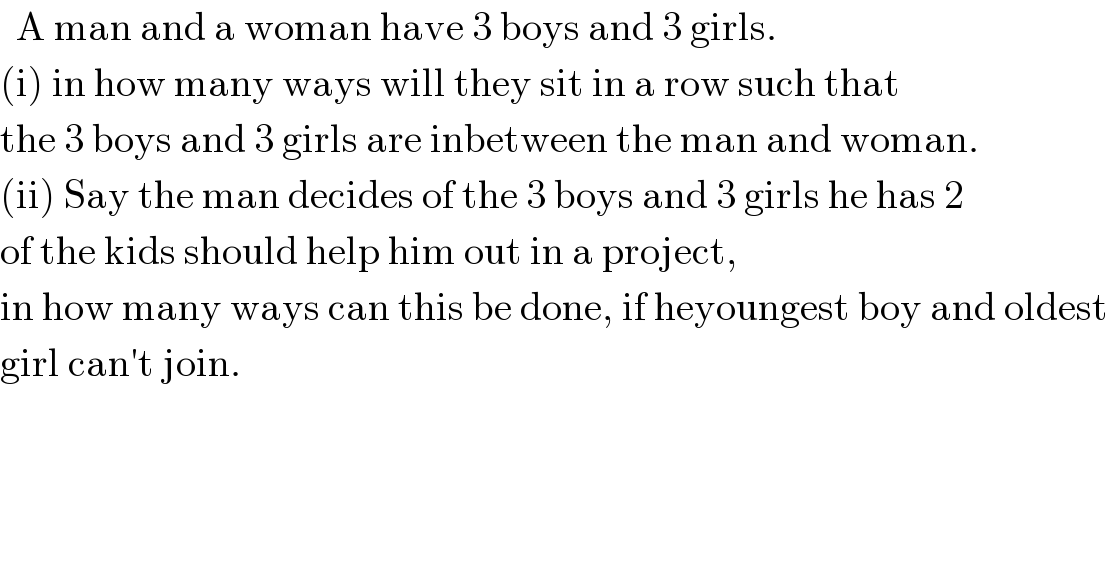
A man and a woman have 3 boys and 3 girls. (i) in how many ways will they sit in a row such that the 3 boys and 3 girls are inbetween the man and woman. (ii) Say the man decides of the 3 boys and 3 girls he has 2 of the kids should help him out in a project, in how many ways can this be done, if heyoungest boy and oldest girl can′t join.
$$\:\:\mathrm{A}\:\mathrm{man}\:\mathrm{and}\:\mathrm{a}\:\mathrm{woman}\:\mathrm{have}\:\mathrm{3}\:\mathrm{boys}\:\mathrm{and}\:\mathrm{3}\:\mathrm{girls}.\: \\ $$$$\left(\mathrm{i}\right)\:\mathrm{in}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{will}\:\mathrm{they}\:\mathrm{sit}\:\mathrm{in}\:\mathrm{a}\:\mathrm{row}\:\mathrm{such}\:\mathrm{that}\: \\ $$$$\mathrm{the}\:\mathrm{3}\:\mathrm{boys}\:\mathrm{and}\:\mathrm{3}\:\mathrm{girls}\:\mathrm{are}\:\mathrm{inbetween}\:\mathrm{the}\:\mathrm{man}\:\mathrm{and}\:\mathrm{woman}. \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{Say}\:\mathrm{the}\:\mathrm{man}\:\mathrm{decides}\:\mathrm{of}\:\mathrm{the}\:\mathrm{3}\:\mathrm{boys}\:\mathrm{and}\:\mathrm{3}\:\mathrm{girls}\:\mathrm{he}\:\mathrm{has}\:\mathrm{2}\: \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{kids}\:\mathrm{should}\:\mathrm{help}\:\mathrm{him}\:\mathrm{out}\:\mathrm{in}\:\mathrm{a}\:\mathrm{project}, \\ $$$$\mathrm{in}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{done},\:\mathrm{if}\:\mathrm{heyoungest}\:\mathrm{boy}\:\mathrm{and}\:\mathrm{oldest} \\ $$$$\mathrm{girl}\:\mathrm{can}'\mathrm{t}\:\mathrm{join}. \\ $$
Answered by john santu last updated on 19/Jun/20
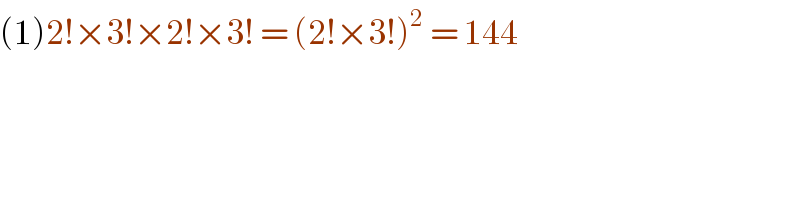
(1)2!×3!×2!×3! = (2!×3!)^2 = 144
$$\left(\mathrm{1}\right)\mathrm{2}!×\mathrm{3}!×\mathrm{2}!×\mathrm{3}!\:=\:\left(\mathrm{2}!×\mathrm{3}!\right)^{\mathrm{2}} \:=\:\mathrm{144}\: \\ $$
Commented by Rio Michael last updated on 19/Jun/20
thanks sir, you got any explanation?
$$\mathrm{thanks}\:\mathrm{sir},\:\mathrm{you}\:\mathrm{got}\:\mathrm{any}\:\mathrm{explanation}? \\ $$
Commented by mr W last updated on 19/Jun/20
i think 2×6!=1440
$${i}\:{think} \\ $$$$\mathrm{2}×\mathrm{6}!=\mathrm{1440} \\ $$
Commented by john santu last updated on 19/Jun/20
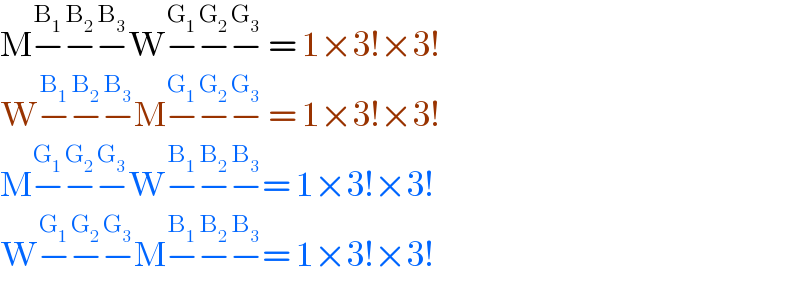
M−^B_1 −^B_2 −^B_3 W−^G_1 −^G_2 −^G_3 = 1×3!×3! W−^B_1 −^B_2 −^B_3 M−^G_1 −^G_2 −^G_3 = 1×3!×3! M−^G_1 −^G_2 −^G_3 W−^B_1 −^B_2 −^B_3 = 1×3!×3! W−^G_1 −^G_2 −^G_3 M−^B_1 −^B_2 −^B_3 = 1×3!×3!
$$\mathrm{M}\overset{\mathrm{B}_{\mathrm{1}} } {−}\overset{\mathrm{B}_{\mathrm{2}} } {−}\overset{\mathrm{B}_{\mathrm{3}} } {−}\mathrm{W}\overset{\mathrm{G}_{\mathrm{1}} } {−}\overset{\mathrm{G}_{\mathrm{2}} } {−}\overset{\mathrm{G}_{\mathrm{3}} } {−}\:=\:\mathrm{1}×\mathrm{3}!×\mathrm{3}!\: \\ $$$$\mathrm{W}\overset{\mathrm{B}_{\mathrm{1}} } {−}\overset{\mathrm{B}_{\mathrm{2}} } {−}\overset{\mathrm{B}_{\mathrm{3}} } {−}\mathrm{M}\overset{\mathrm{G}_{\mathrm{1}} } {−}\overset{\mathrm{G}_{\mathrm{2}} } {−}\overset{\mathrm{G}_{\mathrm{3}} } {−}\:=\:\mathrm{1}×\mathrm{3}!×\mathrm{3}! \\ $$$$\mathrm{M}\overset{\mathrm{G}_{\mathrm{1}} } {−}\overset{\mathrm{G}_{\mathrm{2}} } {−}\overset{\mathrm{G}_{\mathrm{3}} } {−}\mathrm{W}\overset{\mathrm{B}_{\mathrm{1}} } {−}\overset{\mathrm{B}_{\mathrm{2}} } {−}\overset{\mathrm{B}_{\mathrm{3}} } {−}=\:\mathrm{1}×\mathrm{3}!×\mathrm{3}! \\ $$$$\mathrm{W}\overset{\mathrm{G}_{\mathrm{1}} } {−}\overset{\mathrm{G}_{\mathrm{2}} } {−}\overset{\mathrm{G}_{\mathrm{3}} } {−}\mathrm{M}\overset{\mathrm{B}_{\mathrm{1}} } {−}\overset{\mathrm{B}_{\mathrm{2}} } {−}\overset{\mathrm{B}_{\mathrm{3}} } {−}=\:\mathrm{1}×\mathrm{3}!×\mathrm{3}! \\ $$
Commented by john santu last updated on 19/Jun/20
no sir
$$\mathrm{no}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 19/Jun/20
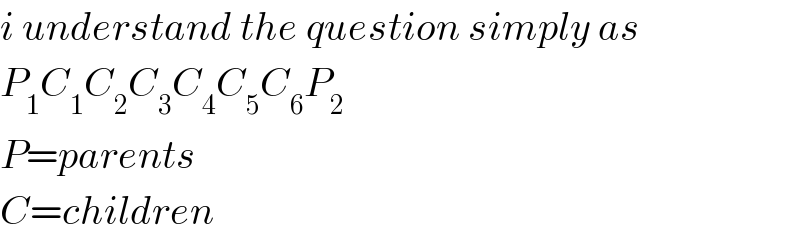
i understand the question simply as P_1 C_1 C_2 C_3 C_4 C_5 C_6 P_2 P=parents C=children
$${i}\:{understand}\:{the}\:{question}\:{simply}\:{as} \\ $$$${P}_{\mathrm{1}} {C}_{\mathrm{1}} {C}_{\mathrm{2}} {C}_{\mathrm{3}} {C}_{\mathrm{4}} {C}_{\mathrm{5}} {C}_{\mathrm{6}} {P}_{\mathrm{2}} \\ $$$${P}={parents} \\ $$$${C}={children} \\ $$
Commented by john santu last updated on 19/Jun/20
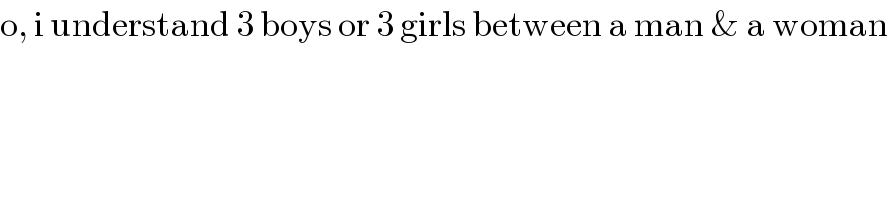
o, i understand 3 boys or 3 girls between a man & a woman
$$\mathrm{o},\:\mathrm{i}\:\mathrm{understand}\:\mathrm{3}\:\mathrm{boys}\:\mathrm{or}\:\mathrm{3}\:\mathrm{girls}\:\mathrm{between}\:\mathrm{a}\:\mathrm{man}\:\&\:\mathrm{a}\:\mathrm{woman} \\ $$
Answered by john santu last updated on 19/Jun/20
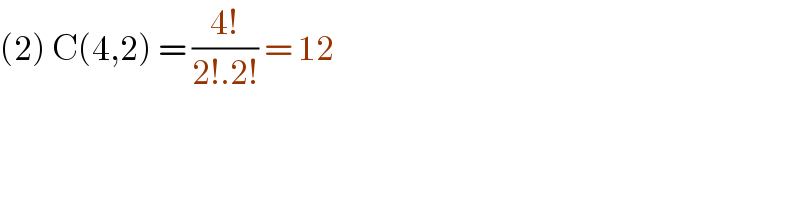
(2) C(4,2) = ((4!)/(2!.2!)) = 12
$$\left(\mathrm{2}\right)\:\mathrm{C}\left(\mathrm{4},\mathrm{2}\right)\:=\:\frac{\mathrm{4}!}{\mathrm{2}!.\mathrm{2}!}\:=\:\mathrm{12}\: \\ $$
Commented by Rio Michael last updated on 19/Jun/20
thanks you′all
$$\mathrm{thanks}\:\mathrm{you}'\mathrm{all} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *