Menu Close

a-man-hits-a-golf-ball-at-the-top-of-a-cliff-which-is-40-0-m-high-given-that-the-ball-falls-into-a-water-down-cliff-and-he-hears-the-sound-3-s-after-he-hit-the-ball-what-is-the-initial-speed-of-the-

Tinku Tara 0 Comments
Pin




Question Number 114850 by Rio Michael last updated on 21/Sep/20
a man hits a golf ball at the top of a cliff which is 40.0 m high. given that the ball falls into a water down cliff and he hears the sound 3 s after he hit the ball. what is the initial speed of the ball. take the speed of sound in air as 343 m/s. neglect air resistance.
$$\mathrm{a}\:\mathrm{man}\:\mathrm{hits}\:\mathrm{a}\:\mathrm{golf}\:\mathrm{ball}\:\mathrm{at}\:\mathrm{the}\:\mathrm{top}\:\mathrm{of}\:\mathrm{a}\:\mathrm{cliff} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{40}.\mathrm{0}\:\mathrm{m}\:\mathrm{high}.\:\mathrm{given}\:\mathrm{that}\:\mathrm{the} \\ $$$$\mathrm{ball}\:\mathrm{falls}\:\mathrm{into}\:\mathrm{a}\:\mathrm{water}\:\mathrm{down}\:\mathrm{cliff}\:\mathrm{and}\:\mathrm{he} \\ $$$$\mathrm{hears}\:\mathrm{the}\:\mathrm{sound}\:\mathrm{3}\:\mathrm{s}\:\mathrm{after}\:\mathrm{he}\:\mathrm{hit}\:\mathrm{the}\:\mathrm{ball}. \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{initial}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ball}.\:\mathrm{take} \\ $$$$\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{sound}\:\mathrm{in}\:\mathrm{air}\:\mathrm{as}\:\mathrm{343}\:\mathrm{m}/\mathrm{s}.\:\mathrm{neglect} \\ $$$$\mathrm{air}\:\mathrm{resistance}. \\ $$
Commented by Dwaipayan Shikari last updated on 21/Sep/20
Time to fall =(√((2h)/g)) =(√8) sec v.(√8) =horizontal distance covered v(√8) =343.(3−(√8)) (Distance traveled by sound wave) v=((343(3−(√8)))/( (√8))) (m/s) v=20.8064(m/s)
$${Time}\:{to}\:{fall}\:=\sqrt{\frac{\mathrm{2}{h}}{{g}}}\:=\sqrt{\mathrm{8}}\:{sec} \\ $$$${v}.\sqrt{\mathrm{8}}\:={horizontal}\:{distance}\:{covered} \\ $$$${v}\sqrt{\mathrm{8}}\:=\mathrm{343}.\left(\mathrm{3}−\sqrt{\mathrm{8}}\right)\:\:\:\left({Distance}\:{traveled}\:{by}\:{sound}\:{wave}\right) \\ $$$${v}=\frac{\mathrm{343}\left(\mathrm{3}−\sqrt{\mathrm{8}}\right)}{\:\sqrt{\mathrm{8}}}\:\frac{{m}}{{s}} \\ $$$${v}=\mathrm{20}.\mathrm{8064}\frac{{m}}{{s}} \\ $$
Answered by Rio Michael last updated on 21/Sep/20
this is my try to the problem. though am not 100% sure , so, please correct me. time taken for sound to reach ears t_1 = ((40.0 m)/(343 m/s)) = 0.12 s ⇒ time of flight = 3.0 s − 0=12 s = 2.88 s range x = v_0 t ; x = 2.88v_0 .....(i) using y = (tan θ_0 )x − (g/(v_0 ^2 cos^2 θ_0 )) x^2 .....(ii) (i) in (ii) with θ_0 = 0° (horizontal hit) ⇒ 40.0 m = 0− (g/v_0 ^2 ) (2.88v_0 )^2 at this points its error. any ideas please
$$\mathrm{this}\:\mathrm{is}\:\mathrm{my}\:\mathrm{try}\:\mathrm{to}\:\mathrm{the}\:\mathrm{problem}.\:\mathrm{though}\: \\ $$$$\mathrm{am}\:\mathrm{not}\:\mathrm{100\%}\:\mathrm{sure}\:,\:\mathrm{so},\:\mathrm{please}\:\mathrm{correct}\:\mathrm{me}. \\ $$$$\:\mathrm{time}\:\mathrm{taken}\:\mathrm{for}\:\mathrm{sound}\:\mathrm{to}\:\mathrm{reach}\:\mathrm{ears}\:{t}_{\mathrm{1}} \:= \\ $$$$\:\frac{\mathrm{40}.\mathrm{0}\:\mathrm{m}}{\mathrm{343}\:\mathrm{m}/\mathrm{s}}\:=\:\mathrm{0}.\mathrm{12}\:\mathrm{s} \\ $$$$\Rightarrow\:\mathrm{time}\:\mathrm{of}\:\mathrm{flight}\:=\:\mathrm{3}.\mathrm{0}\:\mathrm{s}\:−\:\mathrm{0}=\mathrm{12}\:\mathrm{s}\:=\:\mathrm{2}.\mathrm{88}\:\mathrm{s} \\ $$$$\mathrm{range}\:{x}\:=\:{v}_{\mathrm{0}} {t}\:;\:{x}\:=\:\mathrm{2}.\mathrm{88}{v}_{\mathrm{0}} \:…..\left({i}\right) \\ $$$$\mathrm{using}\:{y}\:=\:\left(\mathrm{tan}\:\theta_{\mathrm{0}} \right){x}\:−\:\frac{\mathrm{g}}{{v}_{\mathrm{0}} ^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta_{\mathrm{0}} }\:{x}^{\mathrm{2}} \:…..\left({ii}\right) \\ $$$$\left({i}\right)\:\mathrm{in}\:\left({ii}\right)\:\mathrm{with}\:\theta_{\mathrm{0}} \:=\:\mathrm{0}°\:\left(\mathrm{horizontal}\:\mathrm{hit}\right) \\ $$$$\Rightarrow\:\mathrm{40}.\mathrm{0}\:\mathrm{m}\:=\:\mathrm{0}−\:\frac{\mathrm{g}}{{v}_{\mathrm{0}} ^{\mathrm{2}} }\:\left(\mathrm{2}.\mathrm{88}{v}_{\mathrm{0}} \right)^{\mathrm{2}} \\ $$$$\:\:\mathrm{at}\:\mathrm{this}\:\mathrm{points}\:\mathrm{its}\:\mathrm{error}.\:\mathrm{any}\:\mathrm{ideas}\:\mathrm{please} \\ $$
Answered by mr W last updated on 21/Sep/20
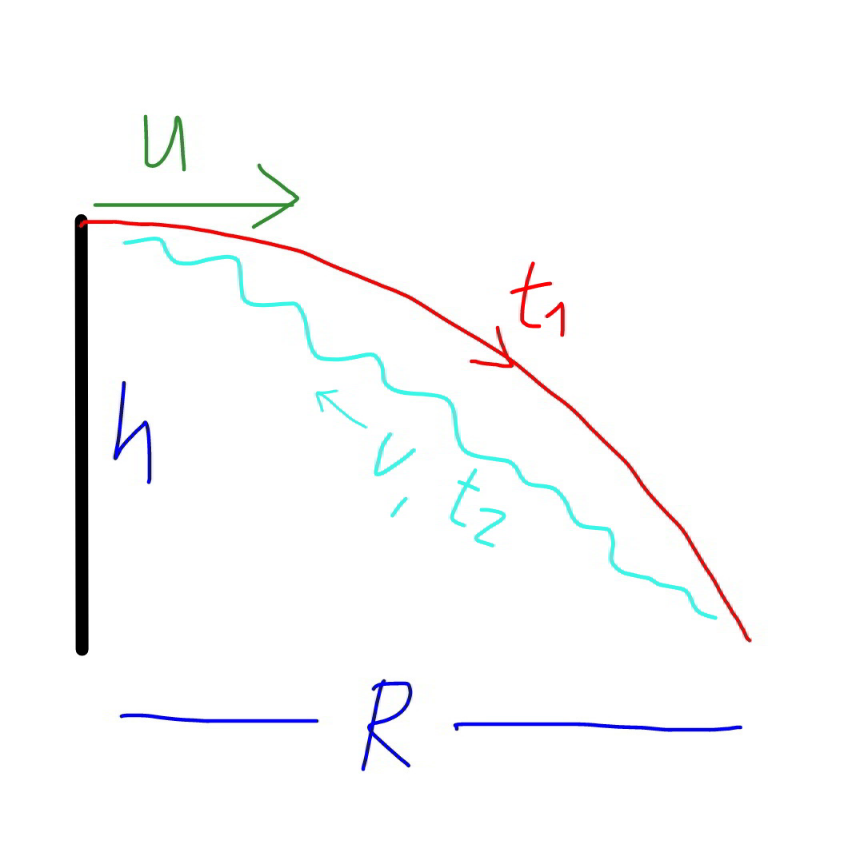
Commented by mr W last updated on 21/Sep/20
time of ball in flight: t_1 =(√((2h)/g)) R=ut_1 =u(√((2h)/g)) time of sound in air: t_2 =((√(h^2 +R^2 ))/v) t_1 +t_2 =t=3 (√((2h)/g))+((√(h^2 +R^2 ))/v)=t (√((2h)/g))+(1/v)(√(h^2 +u^2 ×((2h)/g)))=t u=(√([(t−(√((2h)/g)))^2 v^2 −h^2 ](g/(2h)))) u=(√([(3−(√((2×40)/(10))))^2 ×343^2 −40^2 ]((10)/(2×40)))) =20.8 m/s
$${time}\:{of}\:{ball}\:{in}\:{flight}: \\ $$$${t}_{\mathrm{1}} =\sqrt{\frac{\mathrm{2}{h}}{{g}}} \\ $$$${R}={ut}_{\mathrm{1}} ={u}\sqrt{\frac{\mathrm{2}{h}}{{g}}} \\ $$$${time}\:{of}\:{sound}\:{in}\:{air}: \\ $$$${t}_{\mathrm{2}} =\frac{\sqrt{{h}^{\mathrm{2}} +{R}^{\mathrm{2}} }}{{v}} \\ $$$${t}_{\mathrm{1}} +{t}_{\mathrm{2}} ={t}=\mathrm{3} \\ $$$$\sqrt{\frac{\mathrm{2}{h}}{{g}}}+\frac{\sqrt{{h}^{\mathrm{2}} +{R}^{\mathrm{2}} }}{{v}}={t} \\ $$$$\sqrt{\frac{\mathrm{2}{h}}{{g}}}+\frac{\mathrm{1}}{{v}}\sqrt{{h}^{\mathrm{2}} +{u}^{\mathrm{2}} ×\frac{\mathrm{2}{h}}{{g}}}={t} \\ $$$${u}=\sqrt{\left[\left({t}−\sqrt{\frac{\mathrm{2}{h}}{{g}}}\right)^{\mathrm{2}} {v}^{\mathrm{2}} −{h}^{\mathrm{2}} \right]\frac{{g}}{\mathrm{2}{h}}} \\ $$$${u}=\sqrt{\left[\left(\mathrm{3}−\sqrt{\frac{\mathrm{2}×\mathrm{40}}{\mathrm{10}}}\right)^{\mathrm{2}} ×\mathrm{343}^{\mathrm{2}} −\mathrm{40}^{\mathrm{2}} \right]\frac{\mathrm{10}}{\mathrm{2}×\mathrm{40}}} \\ $$$$=\mathrm{20}.\mathrm{8}\:{m}/{s} \\ $$
Commented by Rio Michael last updated on 22/Sep/20
thank you sir, but i didnt understand a thing
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{i}\:\mathrm{didnt}\:\mathrm{understand} \\ $$$$\mathrm{a}\:\mathrm{thing} \\ $$
Commented by mr W last updated on 22/Sep/20
what then?
$${what}\:{then}? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *