Menu Close

A-man-observes-that-when-he-moves-up-a-distance-c-metres-on-a-slope-the-angle-of-depression-of-a-point-on-the-horizontal-plane-from-the-base-of-the-slope-is-30-and-when-he-moves-up-further-a-distan

Tinku Tara 0 Comments
Pin




Question Number 15393 by Tinkutara last updated on 10/Jun/17
A man observes that when he moves up a distance c metres on a slope, the angle of depression of a point on the horizontal plane from the base of the slope is 30°, and when he moves up further a distance c metres, the angle of depression of that point is 45°. The angle of inclination of the slope with the horizontal is?
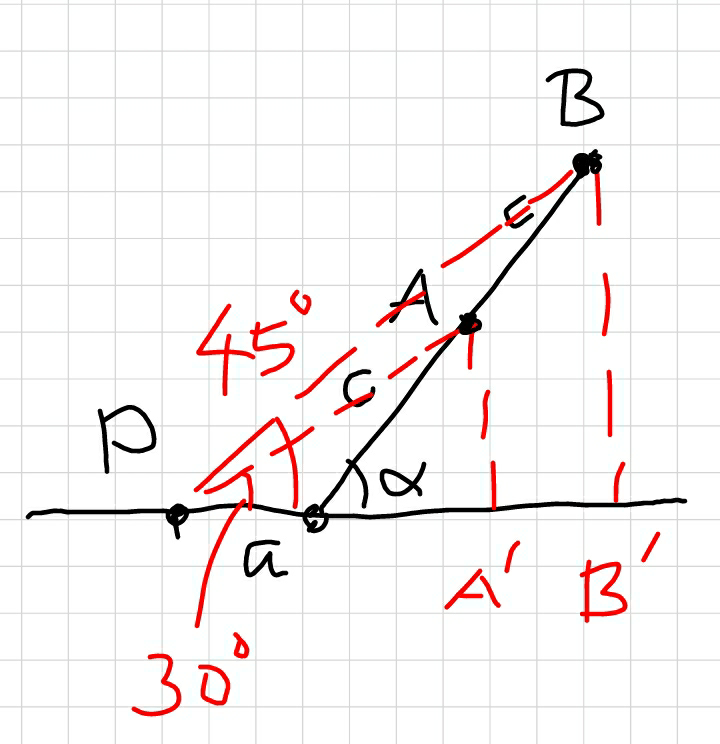
$$\mathrm{A}\:\mathrm{man}\:\mathrm{observes}\:\mathrm{that}\:\mathrm{when}\:\mathrm{he}\:\mathrm{moves}\:\mathrm{up} \\ $$$$\mathrm{a}\:\mathrm{distance}\:{c}\:\mathrm{metres}\:\mathrm{on}\:\mathrm{a}\:\mathrm{slope},\:\mathrm{the} \\ $$$$\mathrm{angle}\:\mathrm{of}\:\mathrm{depression}\:\mathrm{of}\:\mathrm{a}\:\mathrm{point}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{horizontal}\:\mathrm{plane}\:\mathrm{from}\:\mathrm{the}\:\mathrm{base}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{slope}\:\mathrm{is}\:\mathrm{30}°,\:\mathrm{and}\:\mathrm{when}\:\mathrm{he}\:\mathrm{moves}\:\mathrm{up} \\ $$$$\mathrm{further}\:\mathrm{a}\:\mathrm{distance}\:{c}\:\mathrm{metres},\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of} \\ $$$$\mathrm{depression}\:\mathrm{of}\:\mathrm{that}\:\mathrm{point}\:\mathrm{is}\:\mathrm{45}°.\:\mathrm{The} \\ $$$$\mathrm{angle}\:\mathrm{of}\:\mathrm{inclination}\:\mathrm{of}\:\mathrm{the}\:\mathrm{slope}\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{horizontal}\:\mathrm{is}? \\ $$
Answered by mrW1 last updated on 10/Jun/17
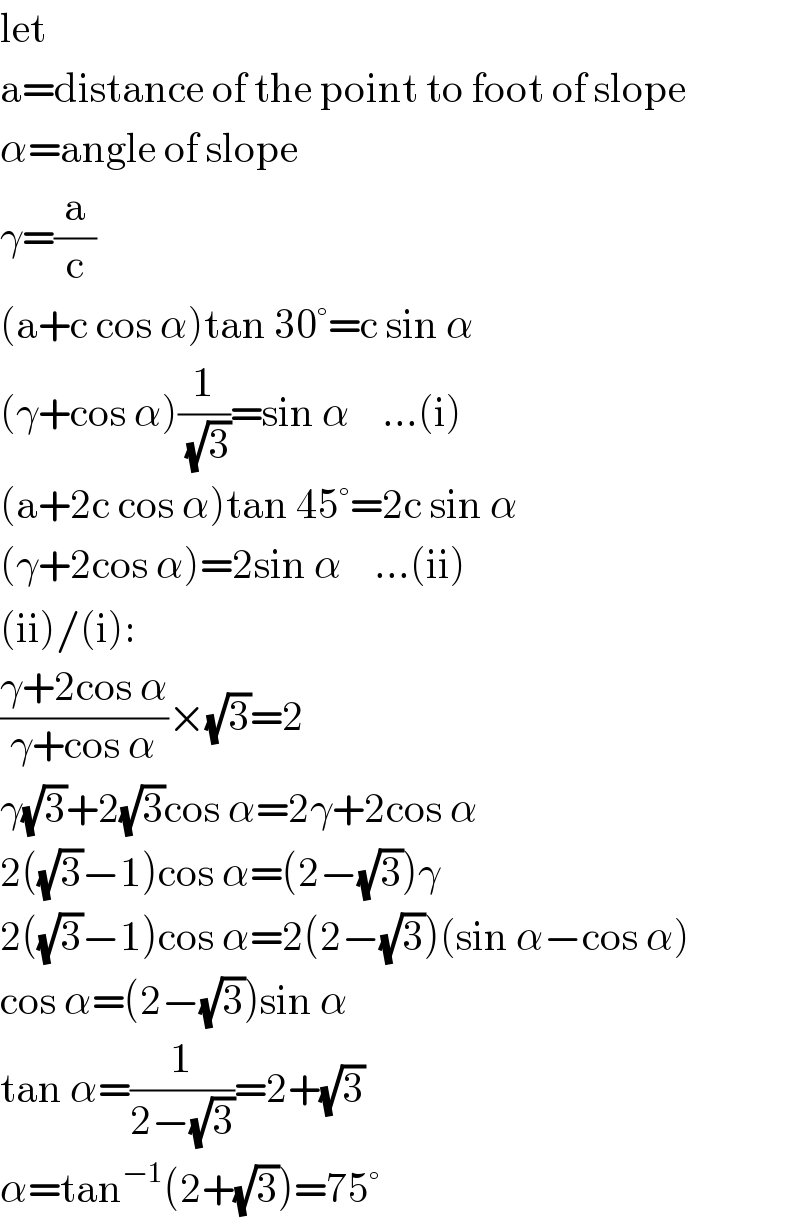
let a=distance of the point to foot of slope α=angle of slope γ=(a/c) (a+c cos α)tan 30°=c sin α (γ+cos α)(1/( (√3)))=sin α ...(i) (a+2c cos α)tan 45°=2c sin α (γ+2cos α)=2sin α ...(ii) (ii)/(i): ((γ+2cos α)/(γ+cos α))×(√3)=2 γ(√3)+2(√3)cos α=2γ+2cos α 2((√3)−1)cos α=(2−(√3))γ 2((√3)−1)cos α=2(2−(√3))(sin α−cos α) cos α=(2−(√3))sin α tan α=(1/(2−(√3)))=2+(√3) α=tan^(−1) (2+(√3))=75°
$$\mathrm{let} \\ $$$$\mathrm{a}=\mathrm{distance}\:\mathrm{of}\:\mathrm{the}\:\mathrm{point}\:\mathrm{to}\:\mathrm{foot}\:\mathrm{of}\:\mathrm{slope} \\ $$$$\alpha=\mathrm{angle}\:\mathrm{of}\:\mathrm{slope} \\ $$$$\gamma=\frac{\mathrm{a}}{\mathrm{c}} \\ $$$$\left(\mathrm{a}+\mathrm{c}\:\mathrm{cos}\:\alpha\right)\mathrm{tan}\:\mathrm{30}°=\mathrm{c}\:\mathrm{sin}\:\alpha \\ $$$$\left(\gamma+\mathrm{cos}\:\alpha\right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\mathrm{sin}\:\alpha\:\:\:\:…\left(\mathrm{i}\right) \\ $$$$\left(\mathrm{a}+\mathrm{2c}\:\mathrm{cos}\:\alpha\right)\mathrm{tan}\:\mathrm{45}°=\mathrm{2c}\:\mathrm{sin}\:\alpha \\ $$$$\left(\gamma+\mathrm{2cos}\:\alpha\right)=\mathrm{2sin}\:\alpha\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{ii}\right)/\left(\mathrm{i}\right): \\ $$$$\frac{\gamma+\mathrm{2cos}\:\alpha}{\gamma+\mathrm{cos}\:\alpha}×\sqrt{\mathrm{3}}=\mathrm{2} \\ $$$$\gamma\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}\mathrm{cos}\:\alpha=\mathrm{2}\gamma+\mathrm{2cos}\:\alpha \\ $$$$\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\mathrm{cos}\:\alpha=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\gamma \\ $$$$\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\mathrm{cos}\:\alpha=\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\left(\mathrm{sin}\:\alpha−\mathrm{cos}\:\alpha\right) \\ $$$$\mathrm{cos}\:\alpha=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{sin}\:\alpha \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{3}}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right)=\mathrm{75}° \\ $$
Commented by mrW1 last updated on 10/Jun/17
Commented by Tinkutara last updated on 10/Jun/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *