Question Number 26450 by Tinkutara last updated on 25/Dec/17

$$\mathrm{A}\:\mathrm{man}\:\mathrm{of}\:\mathrm{mass}\:{M}\:\mathrm{is}\:\mathrm{standing}\:\mathrm{on}\:\mathrm{a} \\ $$$$\mathrm{platform}\:\mathrm{of}\:\mathrm{mass}\:{m}_{\mathrm{1}} \:\mathrm{holding}\:\mathrm{a}\:\mathrm{string} \\ $$$$\mathrm{passing}\:\mathrm{over}\:\mathrm{a}\:\mathrm{system}\:\mathrm{of}\:\mathrm{ideal}\:\mathrm{pulleys}. \\ $$$$\mathrm{Another}\:\mathrm{mass}\:{m}_{\mathrm{2}} \:\mathrm{is}\:\mathrm{hanging}\:\mathrm{as}\:\mathrm{shown} \\ $$$$\left({m}_{\mathrm{2}} \:=\:\mathrm{20}\:\mathrm{kg},\:{m}_{\mathrm{1}} \:=\:\mathrm{10}\:\mathrm{kg},\:{g}\:=\:\mathrm{10}\:\mathrm{m}/\mathrm{s}^{\mathrm{2}} \right) \\ $$$$\mathrm{Force}\:\mathrm{exerted}\:\mathrm{by}\:\mathrm{man}\:\mathrm{on}\:\mathrm{string}\:\mathrm{to} \\ $$$$\mathrm{accelerate}\:\mathrm{upwards} \\ $$
Commented by Tinkutara last updated on 25/Dec/17

Commented by mrW1 last updated on 26/Dec/17
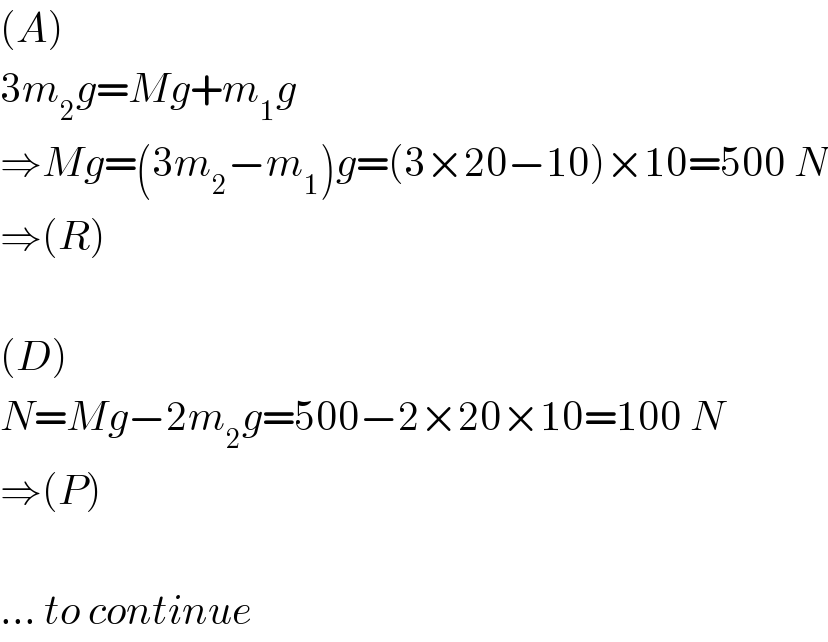
$$\left({A}\right) \\ $$$$\mathrm{3}{m}_{\mathrm{2}} {g}={Mg}+{m}_{\mathrm{1}} {g} \\ $$$$\Rightarrow{Mg}=\left(\mathrm{3}{m}_{\mathrm{2}} −{m}_{\mathrm{1}} \right){g}=\left(\mathrm{3}×\mathrm{20}−\mathrm{10}\right)×\mathrm{10}=\mathrm{500}\:{N} \\ $$$$\Rightarrow\left({R}\right) \\ $$$$ \\ $$$$\left({D}\right) \\ $$$${N}={Mg}−\mathrm{2}{m}_{\mathrm{2}} {g}=\mathrm{500}−\mathrm{2}×\mathrm{20}×\mathrm{10}=\mathrm{100}\:{N} \\ $$$$\Rightarrow\left({P}\right) \\ $$$$ \\ $$$$…\:{to}\:{continue} \\ $$
Commented by Tinkutara last updated on 26/Dec/17

Commented by Tinkutara last updated on 26/Dec/17
Above was the full question. It is a Matrix matching columns. If the image is not clear see it at: http://ibb.co/mVtvPm
Commented by mrW1 last updated on 26/Dec/17

$${thanks}!\:{now}\:{it}'{s}\:{clear}. \\ $$
Answered by ajfour last updated on 26/Dec/17

$${A}\rightarrow{R}\:\: \\ $$$${B}\rightarrow{R},{S},{T} \\ $$$${C}\rightarrow{P},{Q} \\ $$$${D}\rightarrow{P} \\ $$$${Are}\:{they}\:{correct}\:\left({by}\:{any}\:{chance}\right)? \\ $$
Answered by ajfour last updated on 26/Dec/17

Commented by Tinkutara last updated on 27/Dec/17
So force exerted by man should be N? Right?
Commented by Tinkutara last updated on 27/Dec/17
But N and F are different or not?
Commented by ajfour last updated on 27/Dec/17

$${under}\:{equilibrium}\:{of}\:{platform} \\ $$$${T}_{\mathrm{1}} =\frac{{T}_{\mathrm{2}} }{\mathrm{2}}=\frac{{F}}{\mathrm{2}}={N}+{m}_{\mathrm{1}} {g} \\ $$$${so}\:{N}\:{and}\:{F}\:{are}\:{different}. \\ $$
Commented by ajfour last updated on 27/Dec/17
why makes you arrive at this conclusion, do explain.
Commented by Tinkutara last updated on 27/Dec/17
In B question it is asking about force exerted by man on string so it should be the normal reaction that man can exert on string because string is under his feet.
Commented by ajfour last updated on 26/Dec/17

$$\:\left({case}\:{I}\right){system}\:{boundary}\:{includes} \\ $$$${man}\:{and}\:{platform}: \\ $$$$\mathrm{3}{T}_{\mathrm{1}} −\left({M}+\mathrm{10}\right){g}=\mathrm{0}\:\:\:\:…\left({i}\right) \\ $$$${and}\:\:{also}\:\:{T}_{\mathrm{1}} =\mathrm{20}{g}\:\:\:\left({in}\:{equilibrium}\right) \\ $$$$\Rightarrow{M}=\mathrm{50}{kg}\:;\:{W}={Mg}=\mathrm{500}\:{newtons} \\ $$$$\Rightarrow\:\:{A}\rightarrow{R} \\ $$$${when}\:{in}\:{slight}\:{acceleration}\left(\uparrow\right) \\ $$$${F}=\mathrm{2}{T}_{\mathrm{1}} \\ $$$$\mathrm{20}{g}−\frac{{F}}{\mathrm{2}}>\:\mathrm{0}\:\:\:\Rightarrow\:\:{F}\:>\:\mathrm{40}{g}\: \\ $$$$\Rightarrow\:\:{hence}\:{B}\rightarrow\:\:{R},{S},{T} \\ $$$${and}\:{for}\:{slight}\:{acceleration}\:\left(\downarrow\right) \\ $$$${F}\:<\:\mathrm{40}{g} \\ $$$${and}\:\:{C}\rightarrow{P},{Q} \\ $$$${forces}\:{on}\:{platform}\left({in}\:{equilibrium}\right) \\ $$$$\:{T}_{\mathrm{1}} −\mathrm{10}{g}−{N}\:=\mathrm{0} \\ $$$${or}\:\:\frac{{F}}{\mathrm{2}}−\mathrm{10}{g}−{N}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{N}=\:\mathrm{200}−\mathrm{100}\:=\mathrm{100}\:{newtons} \\ $$$${so}\:\:\:{D}\rightarrow{P}\:. \\ $$
Commented by Tinkutara last updated on 27/Dec/17

$${You}\:{wrote}\:{for}\:\left({B}\right)\:{that}\:{F}>\mathrm{40}{g}.\:{But} \\ $$$${force}\:{exerted}\:{by}\:{man}\:{on}\:{string}\:{should} \\ $$$${be}\:{N}\:\left({normal}\:{reaction}\right)\:{instead}\:{of}\:{F} \\ $$$$=\mathrm{2}{T}_{\mathrm{1}} .\:{Please}\:{explain}. \\ $$
Commented by ajfour last updated on 27/Dec/17
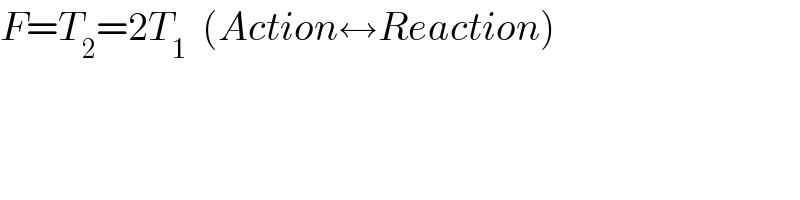
$${F}={T}_{\mathrm{2}} =\mathrm{2}{T}_{\mathrm{1}} \:\:\left({Action}\leftrightarrow{Reaction}\right) \\ $$
Commented by ajfour last updated on 27/Dec/17

$${no}\:{string}\:{under}\:{his}\:{feet},\:{that}\: \\ $$$${string}\:{is}\:{attached}\:{to}\:{platform} \\ $$$${m}_{\mathrm{1}} .\:{The}\:{question}\:{must}\:{be}\:{asking} \\ $$$${for}\:{the}\:{string}\:{he}\:{must}\:{be}\:{holding} \\ $$$${in}\:{hand},\:{which}\:{in}\:{diagram}\:\left({not}\right. \\ $$$$\left.{correctly}\:{drawn}\right)\:{has}\:{been}\:{attached} \\ $$$${to}\:{his}\:{head}.\:{so}\:{F}={T}_{\mathrm{2}} \:\neq{N}\:. \\ $$
Commented by Tinkutara last updated on 27/Dec/17
Thank you very much Sir! I got the answer.
