Question Number 34703 by NECx last updated on 10/May/18

$${A}\:{man}\:{pushes}\:{a}\:{box}\:{of}\:\mathrm{40}{kg}\:{up}\:{an} \\ $$$${incline}\:{of}\:\mathrm{15}°,{if}\:{the}\:{man}\:{applies} \\ $$$${a}\:{horizontal}\:{force}\:\mathrm{200}{N}\:{and}\:{the} \\ $$$${box}\:{moves}\:{up}\:{the}\:{plane}\:{a}\:{distance} \\ $$$${of}\:\mathrm{20}{m}\:{at}\:{a}\:{constant}\:{velocity}\:{and} \\ $$$${the}\:{coefficient}\:{of}\:{friction}\:{is}\:\mathrm{0}.\mathrm{1}, \\ $$$${find}\: \\ $$$$\left.{a}\right){the}\:{workdone}\:{by}\:{the}\:{man}\:{on}\:{the} \\ $$$${box} \\ $$$$\left.{b}\right){workdone}\:{against}\:{friction} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/May/18
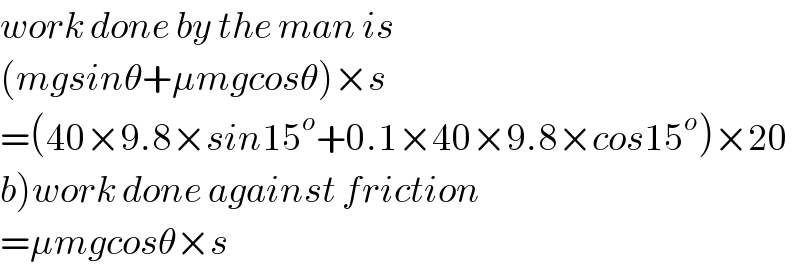
$${work}\:{done}\:{by}\:{the}\:{man}\:{is} \\ $$$$\left({mgsin}\theta+\mu{mgcos}\theta\right)×{s} \\ $$$$=\left(\mathrm{40}×\mathrm{9}.\mathrm{8}×{sin}\mathrm{15}^{{o}} +\mathrm{0}.\mathrm{1}×\mathrm{40}×\mathrm{9}.\mathrm{8}×{cos}\mathrm{15}^{{o}} \right)×\mathrm{20} \\ $$$$\left.{b}\right){work}\:{done}\:{against}\:{friction} \\ $$$$=\mu{mgcos}\theta×{s} \\ $$
