Question Number 114875 by bobhans last updated on 21/Sep/20

$${A}\:{man}\:{sent}\:\mathrm{7}\:{letters}\:{to}\:{his}\:\mathrm{7}\:{friend}\:. \\ $$$${the}\:{letters}\:{are}\:{kept}\:{in}\:{addressed}\:{envelopes} \\ $$$${at}\:{random}.\:{the}\:{probability}\:{that}\:\mathrm{3}\:{friends} \\ $$$${receive}\:{correct}\:{letters}\:{and}\:\mathrm{4}\:{letters}\:{go} \\ $$$${to}\:{wrong}\:{destination}\:{is}\:\_ \\ $$$$ \\ $$$$\left({old}\:{question}\:{unanswered}\right) \\ $$
Answered by PRITHWISH SEN 2 last updated on 21/Sep/20
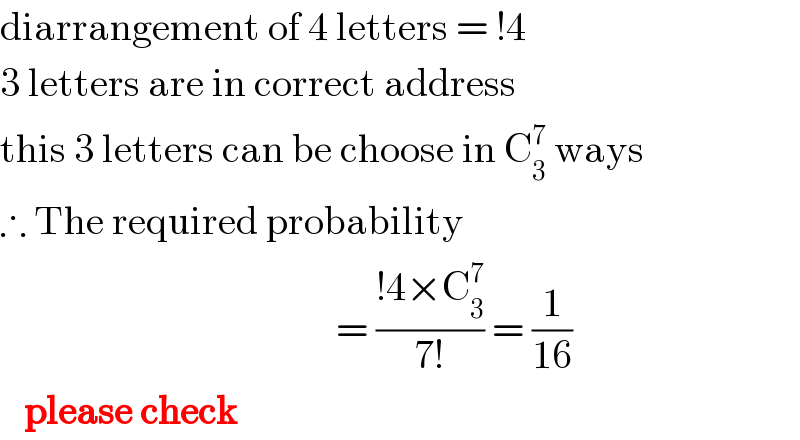
$$\mathrm{diarrangement}\:\mathrm{of}\:\mathrm{4}\:\mathrm{letters}\:=\:!\mathrm{4} \\ $$$$\mathrm{3}\:\mathrm{letters}\:\mathrm{are}\:\mathrm{in}\:\mathrm{correct}\:\mathrm{address} \\ $$$$\mathrm{this}\:\mathrm{3}\:\mathrm{letters}\:\mathrm{can}\:\mathrm{be}\:\mathrm{choose}\:\mathrm{in}\:\mathrm{C}_{\mathrm{3}} ^{\mathrm{7}} \:\mathrm{ways} \\ $$$$\therefore\:\mathrm{The}\:\mathrm{required}\:\mathrm{probability} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{!\mathrm{4}×\mathrm{C}_{\mathrm{3}} ^{\mathrm{7}} }{\mathrm{7}!}\:=\:\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$
Commented by mr W last updated on 21/Sep/20

$${correct}! \\ $$
Commented by PRITHWISH SEN 2 last updated on 21/Sep/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 21/Sep/20
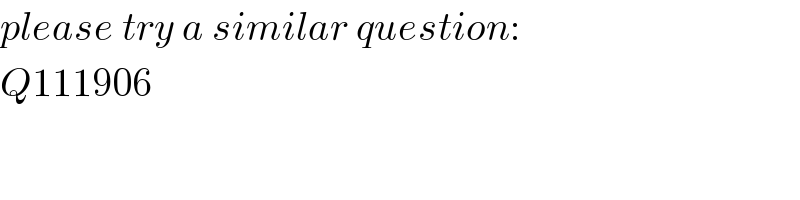
$${please}\:{try}\:{a}\:{similar}\:{question}: \\ $$$${Q}\mathrm{111906} \\ $$
Commented by john santu last updated on 21/Sep/20
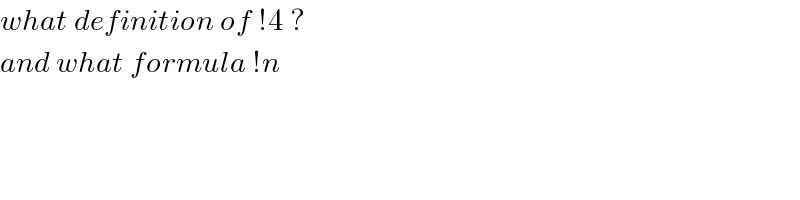
$${what}\:{definition}\:{of}\:!\mathrm{4}\:? \\ $$$${and}\:{what}\:{formula}\:!{n}\: \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Sep/20
![!n = n![1−(1/(1!))+(1/(2!))−(1/(3!))+.......+(−1)^n (1/(n!))]](https://www.tinkutara.com/question/Q114935.png)
$$!\boldsymbol{\mathrm{n}}\:=\:\boldsymbol{\mathrm{n}}!\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+…….+\left(−\mathrm{1}\right)^{\mathrm{n}} \frac{\mathrm{1}}{\mathrm{n}!}\right] \\ $$
Commented by mr W last updated on 27/Sep/20
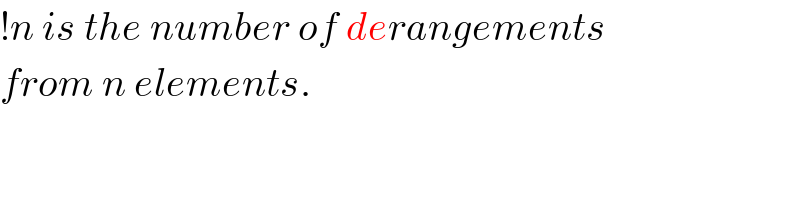
$$!{n}\:{is}\:{the}\:{number}\:{of}\:{derangements} \\ $$$${from}\:{n}\:{elements}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Sep/20

$$\mathrm{sir}\:\mathrm{please}\:\mathrm{check}\:\mathrm{Q}\:\mathrm{111906} \\ $$
Answered by soumyasaha last updated on 22/Sep/20
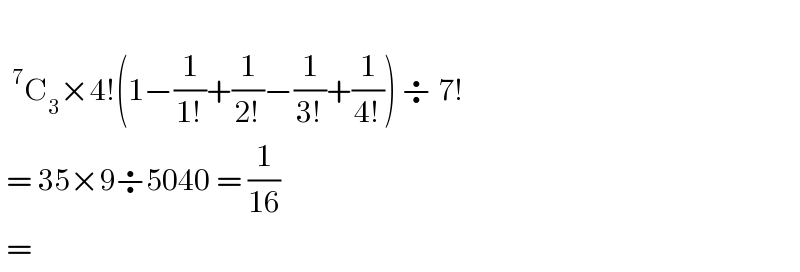
$$ \\ $$$$\:\:^{\mathrm{7}} \mathrm{C}_{\mathrm{3}} ×\mathrm{4}!\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}\right)\:\boldsymbol{\div}\:\mathrm{7}! \\ $$$$\:=\:\mathrm{35}×\mathrm{9}\boldsymbol{\div}\mathrm{5040}\:=\:\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\:=\: \\ $$
