A-mass-10kg-is-placed-at-the-foot-of-an-inclined-plane-13m-long-whose-upper-end-is-5m-higher-than-the-foot-The-mass-is-connected-by-a-light-inextensible-string-passing-over-a-smooth-pulley-at-the-t

Question Number 171627 by Tawa11 last updated on 18/Jun/22

A mass 10kg is placed at the foot of an inclined plane 13m long, whose upper end is 5m higher than the foot. The mass is connected by a light inextensible string, passing over a smooth pulley at the top of the plane, to another mass 10kg which hangs level with the top of the plane, 5m above the floor. If the coefficient of friction between the first mass and then plane is ½ and the system is released from rest, find the acceleration and tension In the string. [Take g = 9.8m/s²]

Commented by mr W last updated on 19/Jun/22

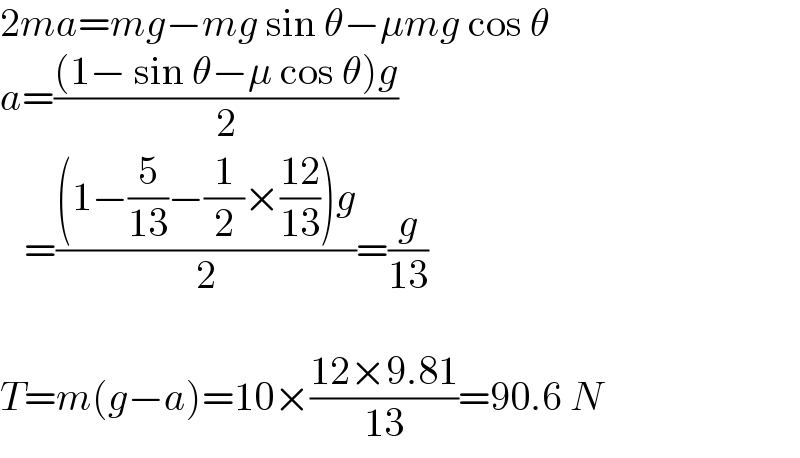
$$\mathrm{2}{ma}={mg}−{mg}\:\mathrm{sin}\:\theta−\mu{mg}\:\mathrm{cos}\:\theta \\ $$$${a}=\frac{\left(\mathrm{1}−\:\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right){g}}{\mathrm{2}} \\ $$$$\:\:\:=\frac{\left(\mathrm{1}−\frac{\mathrm{5}}{\mathrm{13}}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{12}}{\mathrm{13}}\right){g}}{\mathrm{2}}=\frac{{g}}{\mathrm{13}} \\ $$$$ \\ $$$${T}={m}\left({g}−{a}\right)=\mathrm{10}×\frac{\mathrm{12}×\mathrm{9}.\mathrm{81}}{\mathrm{13}}=\mathrm{90}.\mathrm{6}\:{N} \\ $$

Commented by Tawa11 last updated on 19/Jun/22

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 19/Jun/22

$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{I}\:\mathrm{need}\:\mathrm{the}\:\mathrm{diagram}\:\mathrm{interpretation}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$

Commented by mr W last updated on 19/Jun/22

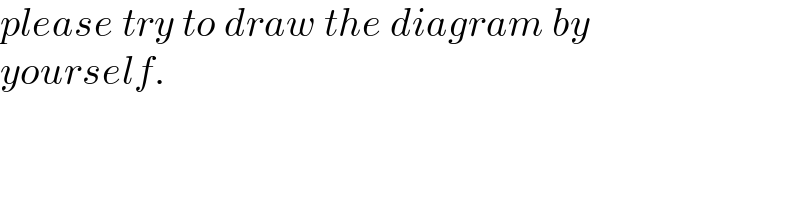
$${please}\:{try}\:{to}\:{draw}\:{the}\:{diagram}\:{by} \\ $$$${yourself}. \\ $$

Commented by Tawa11 last updated on 19/Jun/22

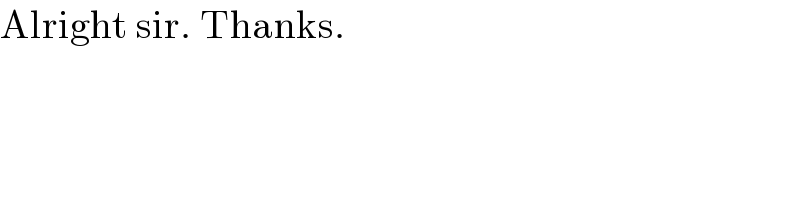
$$\mathrm{Alright}\:\mathrm{sir}.\:\mathrm{Thanks}. \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com