Question Number 22135 by Tinkutara last updated on 11/Oct/17

$$\mathrm{A}\:\mathrm{mass}\:{m}\:\mathrm{hangs}\:\mathrm{with}\:\mathrm{the}\:\mathrm{help}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{string}\:\mathrm{wrapped}\:\mathrm{around}\:\mathrm{a}\:\mathrm{pulley}\:\mathrm{on}\:\mathrm{a} \\ $$$$\mathrm{frictionless}\:\mathrm{bearing}.\:\mathrm{The}\:\mathrm{pulley}\:\mathrm{has} \\ $$$$\mathrm{mass}\:{m}\:\mathrm{and}\:\mathrm{radius}\:{R}.\:\mathrm{Assuming}\:\mathrm{pulley} \\ $$$$\mathrm{to}\:\mathrm{be}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{uniform}\:\mathrm{circular}\:\mathrm{disc},\:\mathrm{the} \\ $$$$\mathrm{acceleration}\:\mathrm{of}\:\mathrm{the}\:\mathrm{mass}\:{m},\:\mathrm{if}\:\mathrm{the} \\ $$$$\mathrm{string}\:\mathrm{does}\:\mathrm{not}\:\mathrm{slip}\:\mathrm{on}\:\mathrm{the}\:\mathrm{pulley},\:\mathrm{is} \\ $$
Answered by ajfour last updated on 11/Oct/17
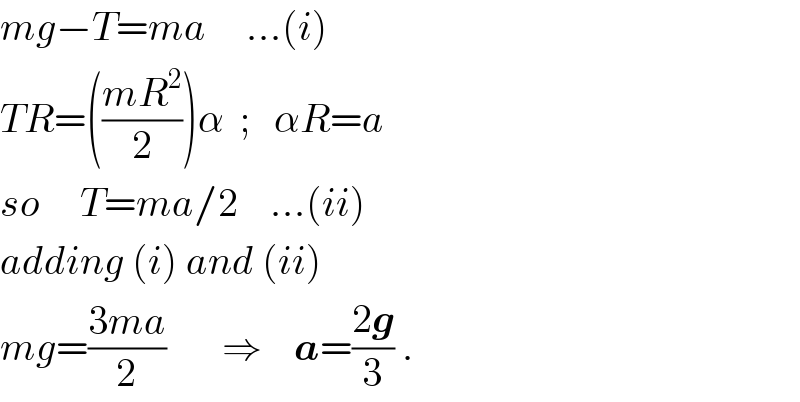
$${mg}−{T}={ma}\:\:\:\:\:…\left({i}\right) \\ $$$${TR}=\left(\frac{{mR}^{\mathrm{2}} }{\mathrm{2}}\right)\alpha\:\:;\:\:\:\alpha{R}={a} \\ $$$${so}\:\:\:\:\:{T}={ma}/\mathrm{2}\:\:\:\:…\left({ii}\right) \\ $$$${adding}\:\left({i}\right)\:{and}\:\left({ii}\right) \\ $$$${mg}=\frac{\mathrm{3}{ma}}{\mathrm{2}}\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\boldsymbol{{a}}=\frac{\mathrm{2}\boldsymbol{{g}}}{\mathrm{3}}\:. \\ $$
Commented by Tinkutara last updated on 11/Oct/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
