Menu Close

A-mass-oscillating-on-a-spring-has-amplitude-of-1-2m-and-a-period-of-2s-Deduce-the-equation-for-the-displacement-x-if-the-timing-starts-at-the-instant-when-the-masd-has-its-maximum-displacement-b-cal

Tinku Tara 0 Comments
Pin




Question Number 32757 by NECx last updated on 01/Apr/18
A mass oscillating on a spring has amplitude of 1.2m and a period of 2s.Deduce the equation for the displacement x if the timing starts at the instant when the masd has its maximum displacement. b)calculate the time interval from t=0 before the displacement is 0.08m
$${A}\:{mass}\:{oscillating}\:{on}\:{a}\:{spring} \\ $$$${has}\:{amplitude}\:{of}\:\mathrm{1}.\mathrm{2}{m}\:{and}\:{a}\:{period} \\ $$$${of}\:\mathrm{2}{s}.{Deduce}\:{the}\:{equation}\:{for} \\ $$$${the}\:{displacement}\:{x}\:{if}\:{the}\:{timing} \\ $$$${starts}\:{at}\:{the}\:{instant}\:{when}\:{the}\:{masd} \\ $$$${has}\:{its}\:{maximum}\:{displacement}. \\ $$$$\left.{b}\right){calculate}\:{the}\:{time}\:{interval}\:{from} \\ $$$${t}=\mathrm{0}\:{before}\:{the}\:{displacement}\:{is} \\ $$$$\mathrm{0}.\mathrm{08}{m} \\ $$$$ \\ $$
Commented by NECx last updated on 01/Apr/18
This was what I did x=Acos ωt (dx/dt)=−Aωsin wt at the maximum displacement dx/dt=0 ∴ 0=−Awsinwt sinwt=0 wt=0,π,2π,.......... since w=2π/T then w=π ∵t={0,1,2,........}s ∵x=1.2cos0 when t=0 x=1.2cosπ when t=1 and so on..... This doesnt seem to me like the right answer so I′m confused.
$${This}\:{was}\:{what}\:{I}\:{did} \\ $$$$ \\ $$$${x}={A}\mathrm{cos}\:\omega{t} \\ $$$$\frac{{dx}}{{dt}}=−{A}\omega\mathrm{sin}\:{wt} \\ $$$${at}\:{the}\:{maximum}\:{displacement} \\ $$$${dx}/{dt}=\mathrm{0} \\ $$$$\therefore\:\mathrm{0}=−{Awsinwt} \\ $$$${sinwt}=\mathrm{0} \\ $$$${wt}=\mathrm{0},\pi,\mathrm{2}\pi,………. \\ $$$${since}\:{w}=\mathrm{2}\pi/{T} \\ $$$${then}\:{w}=\pi \\ $$$$\because{t}=\left\{\mathrm{0},\mathrm{1},\mathrm{2},……..\right\}{s} \\ $$$$ \\ $$$$\because{x}=\mathrm{1}.\mathrm{2}{cos}\mathrm{0}\:\:\:\:\:\:\:\:{when}\:{t}=\mathrm{0} \\ $$$$ \\ $$$${x}=\mathrm{1}.\mathrm{2}{cos}\pi\:\:\:\:\:\:{when}\:{t}=\mathrm{1} \\ $$$$ \\ $$$${and}\:{so}\:{on}…..\: \\ $$$${This}\:{doesnt}\:{seem}\:{to}\:{me}\:{like}\:{the} \\ $$$${right}\:{answer}\:{so}\:{I}'{m}\:{confused}. \\ $$
Commented by NECx last updated on 02/Apr/18
someone please help.Please I′ve been struggling with it for a long while
$${someone}\:{please}\:{help}.{Please}\:{I}'{ve} \\ $$$${been}\:{struggling}\:{with}\:{it}\:{for}\:{a}\:{long}\:{while} \\ $$
Commented by NECx last updated on 02/Apr/18
I think Mrw2 and Ajfour have not been online. Really obvious.
$${I}\:{think}\:{Mrw}\mathrm{2}\:{and}\:{Ajfour} \\ $$$$\:{have}\:{not}\:{been}\:{online}. \\ $$$${Really}\:{obvious}. \\ $$
Commented by float last updated on 03/Apr/18
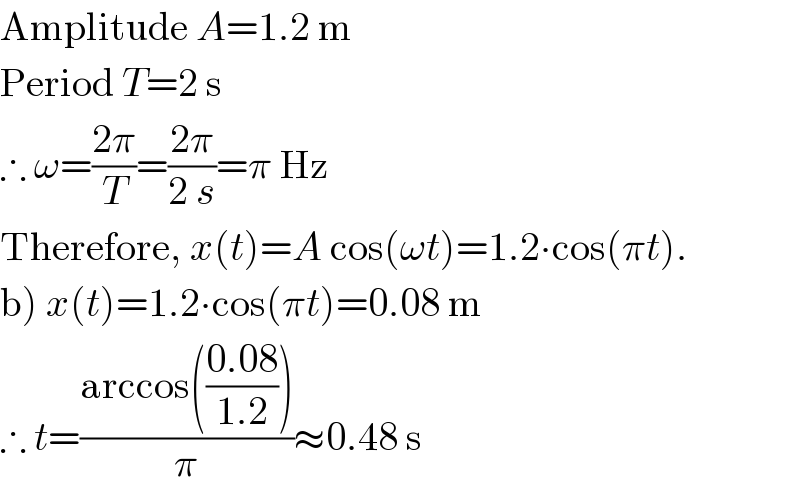
Amplitude A=1.2 m Period T=2 s ∴ ω=((2π)/T)=((2π)/(2 s))=π Hz Therefore, x(t)=A cos(ωt)=1.2∙cos(πt). b) x(t)=1.2∙cos(πt)=0.08 m ∴ t=((arccos(((0.08)/(1.2))))/π)≈0.48 s
$$\mathrm{Amplitude}\:{A}=\mathrm{1}.\mathrm{2}\:\mathrm{m} \\ $$$$\mathrm{Period}\:{T}=\mathrm{2}\:\mathrm{s} \\ $$$$\therefore\:\omega=\frac{\mathrm{2}\pi}{{T}}=\frac{\mathrm{2}\pi}{\mathrm{2}\:{s}}=\pi\:\mathrm{Hz} \\ $$$$\mathrm{Therefore},\:{x}\left({t}\right)={A}\:\mathrm{cos}\left(\omega{t}\right)=\mathrm{1}.\mathrm{2}\centerdot\mathrm{cos}\left(\pi{t}\right). \\ $$$$\left.\mathrm{b}\right)\:{x}\left({t}\right)=\mathrm{1}.\mathrm{2}\centerdot\mathrm{cos}\left(\pi{t}\right)=\mathrm{0}.\mathrm{08}\:\mathrm{m} \\ $$$$\therefore\:{t}=\frac{\mathrm{arccos}\left(\frac{\mathrm{0}.\mathrm{08}}{\mathrm{1}.\mathrm{2}}\right)}{\pi}\approx\mathrm{0}.\mathrm{48}\:\mathrm{s} \\ $$
Commented by NECx last updated on 03/Apr/18
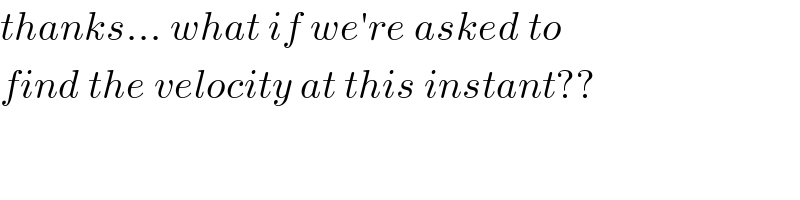
thanks... what if we′re asked to find the velocity at this instant??
$${thanks}…\:{what}\:{if}\:{we}'{re}\:{asked}\:{to} \\ $$$${find}\:{the}\:{velocity}\:{at}\:{this}\:{instant}?? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/May/18
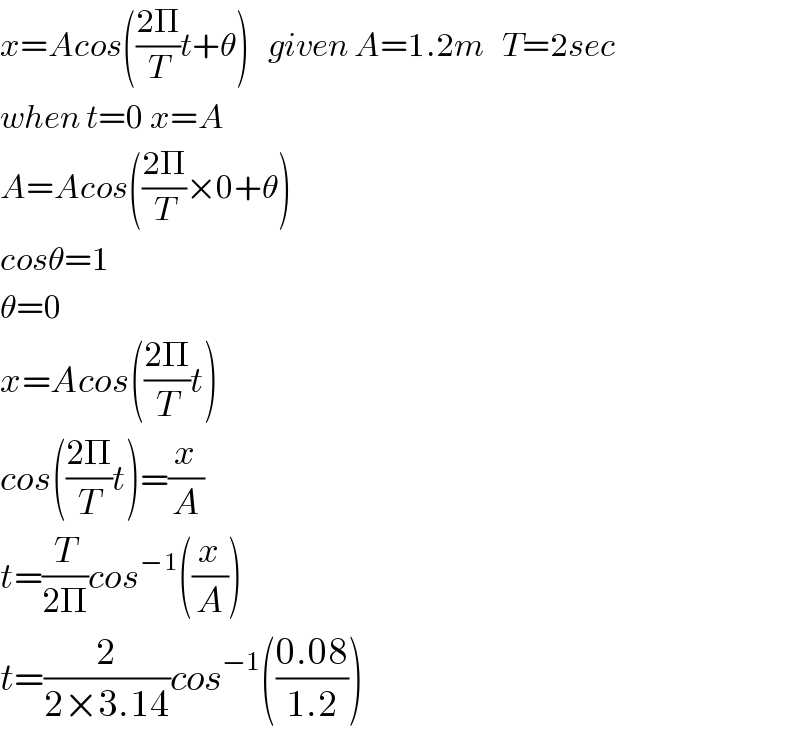
x=Acos(((2Π)/T)t+θ) given A=1.2m T=2sec when t=0 x=A A=Acos(((2Π)/T)×0+θ) cosθ=1 θ=0 x=Acos(((2Π)/T)t) cos(((2Π)/T)t)=(x/A) t=(T/(2Π))cos^(−1) ((x/A)) t=(2/(2×3.14))cos^(−1) (((0.08)/(1.2)))
$${x}={Acos}\left(\frac{\mathrm{2}\Pi}{{T}}{t}+\theta\right)\:\:\:{given}\:{A}=\mathrm{1}.\mathrm{2}{m}\:\:\:{T}=\mathrm{2}{sec} \\ $$$${when}\:{t}=\mathrm{0}\:{x}={A} \\ $$$${A}={Acos}\left(\frac{\mathrm{2}\Pi}{{T}}×\mathrm{0}+\theta\right) \\ $$$${cos}\theta=\mathrm{1} \\ $$$$\theta=\mathrm{0} \\ $$$${x}={Acos}\left(\frac{\mathrm{2}\Pi}{{T}}{t}\right) \\ $$$${cos}\left(\frac{\mathrm{2}\Pi}{{T}}{t}\right)=\frac{{x}}{{A}} \\ $$$${t}=\frac{{T}}{\mathrm{2}\Pi}{cos}^{−\mathrm{1}} \left(\frac{{x}}{{A}}\right) \\ $$$${t}=\frac{\mathrm{2}}{\mathrm{2}×\mathrm{3}.\mathrm{14}}{cos}^{−\mathrm{1}} \left(\frac{\mathrm{0}.\mathrm{08}}{\mathrm{1}.\mathrm{2}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *