Question Number 100664 by bobhans last updated on 28/Jun/20
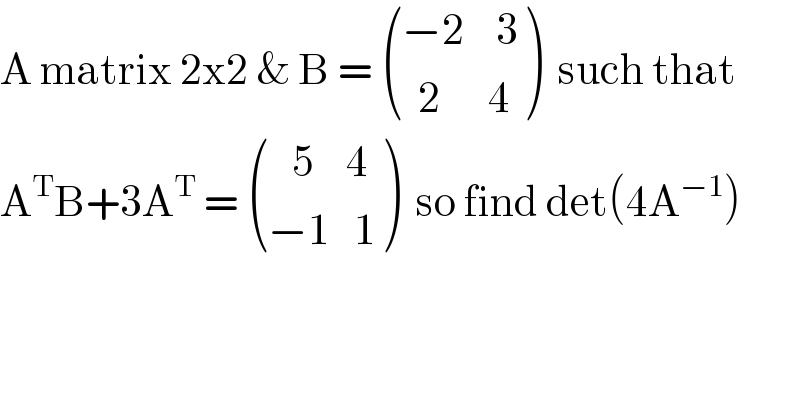
$$\mathrm{A}\:\mathrm{matrix}\:\mathrm{2×2}\:\&\:\mathrm{B}\:=\:\begin{pmatrix}{−\mathrm{2}\:\:\:\:\mathrm{3}}\\{\:\:\mathrm{2}\:\:\:\:\:\:\mathrm{4}}\end{pmatrix}\:\:\mathrm{such}\:\mathrm{that}\: \\ $$$$\mathrm{A}^{\mathrm{T}} \mathrm{B}+\mathrm{3A}^{\mathrm{T}} \:=\:\begin{pmatrix}{\:\:\:\mathrm{5}\:\:\:\:\mathrm{4}}\\{−\mathrm{1}\:\:\:\mathrm{1}}\end{pmatrix}\:\:\mathrm{so}\:\mathrm{find}\:\mathrm{det}\left(\mathrm{4A}^{−\mathrm{1}} \right) \\ $$
Answered by bramlex last updated on 28/Jun/20
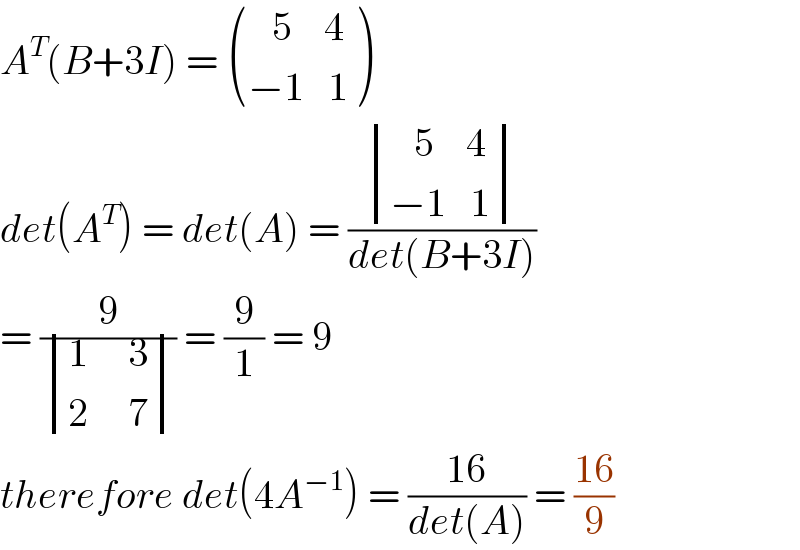
$${A}^{{T}} \left({B}+\mathrm{3}{I}\right)\:=\:\begin{pmatrix}{\:\:\:\mathrm{5}\:\:\:\:\mathrm{4}}\\{−\mathrm{1}\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${det}\left({A}^{{T}} \right)\:=\:{det}\left({A}\right)\:=\:\frac{\begin{vmatrix}{\:\:\:\mathrm{5}\:\:\:\:\mathrm{4}}\\{−\mathrm{1}\:\:\:\mathrm{1}}\end{vmatrix}}{{det}\left({B}+\mathrm{3}{I}\right)} \\ $$$$=\:\frac{\mathrm{9}}{\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{3}}\\{\mathrm{2}\:\:\:\:\:\mathrm{7}}\end{vmatrix}}\:=\:\frac{\mathrm{9}}{\mathrm{1}}\:=\:\mathrm{9} \\ $$$${therefore}\:{det}\left(\mathrm{4}{A}^{−\mathrm{1}} \right)\:=\:\frac{\mathrm{16}}{{det}\left({A}\right)}\:=\:\frac{\mathrm{16}}{\mathrm{9}} \\ $$
