Question Number 13091 by tawa tawa last updated on 13/May/17

$$\mathrm{A}\:\mathrm{motor}\:\mathrm{car}\:\mathrm{moves}\:\mathrm{with}\:\mathrm{a}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{20m}/\mathrm{s}\:\mathrm{on}\:\mathrm{a}\:\mathrm{rough}\:\mathrm{horizontal}\:\mathrm{road}\:\mathrm{and} \\ $$$$\mathrm{covers}\:\mathrm{a}\:\mathrm{displacement}\:\mathrm{of}\:\mathrm{50m}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{dynamic}\:\mathrm{friction}\:\mathrm{between} \\ $$$$\mathrm{the}\:\mathrm{tyre}\:\mathrm{and}\:\mathrm{the}\:\mathrm{ground}\:\:\left(\mathrm{g}\:=\:\mathrm{10m}/\mathrm{s}^{\mathrm{2}} \right). \\ $$
Answered by mrW1 last updated on 14/May/17
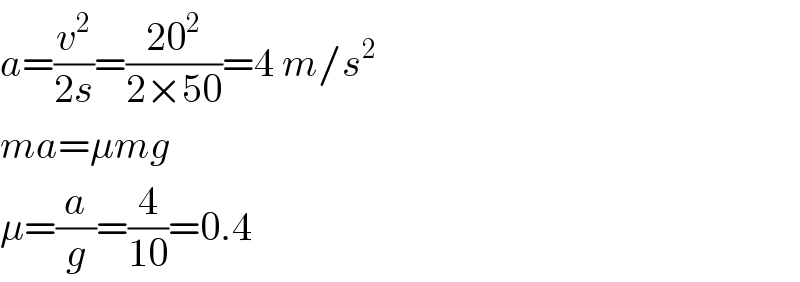
$${a}=\frac{{v}^{\mathrm{2}} }{\mathrm{2}{s}}=\frac{\mathrm{20}^{\mathrm{2}} }{\mathrm{2}×\mathrm{50}}=\mathrm{4}\:{m}/{s}^{\mathrm{2}} \\ $$$${ma}=\mu{mg} \\ $$$$\mu=\frac{{a}}{{g}}=\frac{\mathrm{4}}{\mathrm{10}}=\mathrm{0}.\mathrm{4} \\ $$
Commented by tawa tawa last updated on 14/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
