a-n-1-b-n-1-a-n-b-n-ab-find-n-

Question Number 178240 by Shrinava last updated on 14/Oct/22

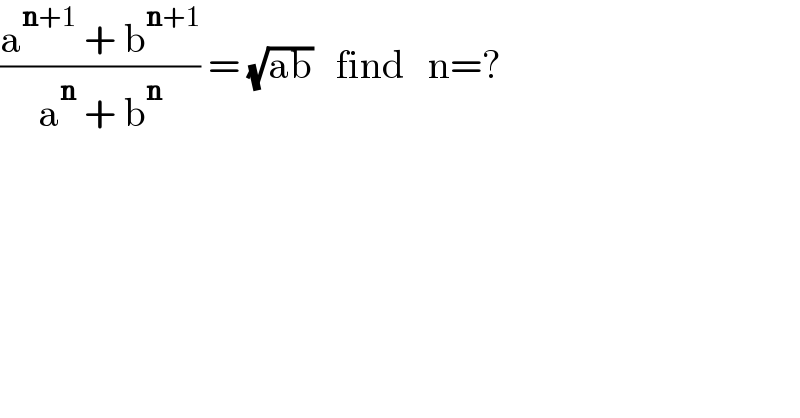
$$\frac{\mathrm{a}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:+\:\mathrm{b}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} }{\mathrm{a}^{\boldsymbol{\mathrm{n}}} \:+\:\mathrm{b}^{\boldsymbol{\mathrm{n}}} }\:=\:\sqrt{\mathrm{ab}}\:\:\:\mathrm{find}\:\:\:\mathrm{n}=? \\ $$

Answered by Rasheed.Sindhi last updated on 14/Oct/22

a^(n+1) + b^(n+1) =a^(1/2) b^(1/2) (a^n + b^n ) a^(n+1) + b^(n+1) =a^(n+(1/2)) b^(1/2) + a^(1/2) b^(n+(1/2)) a^(n+1) −a^(n+(1/2)) b^(1/2) =a^(1/2) b^(n+(1/2)) −b^(n+1) a^(n+(1/2)) (a^(1/2) −b^(1/2) )^(×) =b^(n+(1/2)) (a^(1/2) −b^(1/2) )^(×) [a≠b] a^(n+(1/2)) =b^(n+(1/2)) ((a/b))^(n+(1/2)) =1=((a/b))^0 n+(1/2)=0 n=−(1/2)

$$\mathrm{a}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:+\:\mathrm{b}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} =\mathrm{a}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left(\mathrm{a}^{\boldsymbol{\mathrm{n}}} \:+\:\mathrm{b}^{\boldsymbol{\mathrm{n}}} \right) \\ $$$$\mathrm{a}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:+\:\mathrm{b}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} =\mathrm{a}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\:\mathrm{a}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{b}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{a}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} −\mathrm{a}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{b}^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{a}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{b}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{b}^{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{a}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} \overset{×} {\left(\mathrm{a}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)}=\mathrm{b}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} \overset{×} {\left(\mathrm{a}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)}\:\left[\mathrm{a}\neq\mathrm{b}\right] \\ $$$$\mathrm{a}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{b}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1}=\left(\frac{\mathrm{a}}{\mathrm{b}}\right)^{\mathrm{0}} \\ $$$$\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{n}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by mr W last updated on 14/Oct/22