Question Number 31990 by gunawan last updated on 17/Mar/18
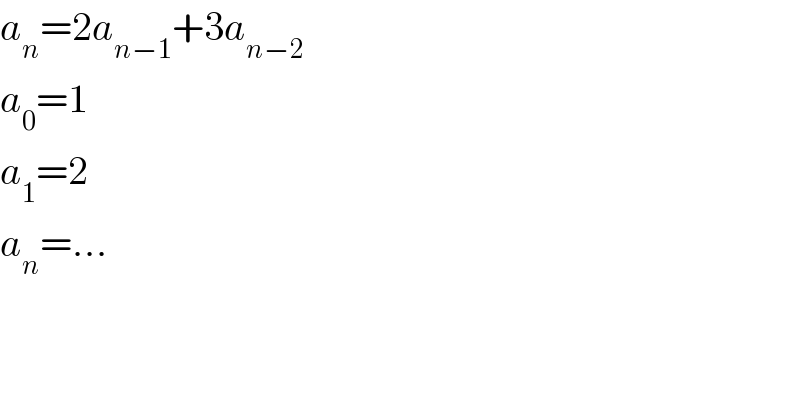
$${a}_{{n}} =\mathrm{2}{a}_{{n}−\mathrm{1}} +\mathrm{3}{a}_{{n}−\mathrm{2}} \\ $$$${a}_{\mathrm{0}} =\mathrm{1} \\ $$$${a}_{\mathrm{1}} =\mathrm{2} \\ $$$${a}_{{n}} =… \\ $$
Commented by mondodotto@gmail.com last updated on 18/Mar/18
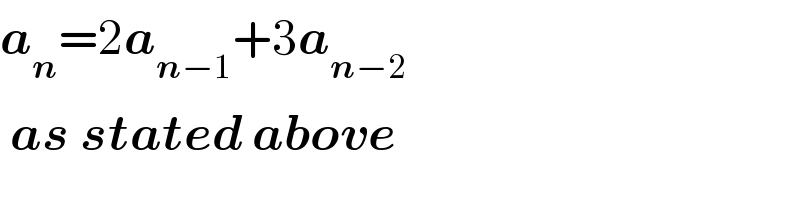
$$\boldsymbol{{a}}_{\boldsymbol{{n}}} =\mathrm{2}\boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{1}} +\mathrm{3}\boldsymbol{{a}}_{\boldsymbol{{n}}−\mathrm{2}} \\ $$$$\:\boldsymbol{{as}}\:\boldsymbol{{stated}}\:\boldsymbol{{above}} \\ $$
Commented by Tinkutara last updated on 18/Mar/18
![a_n =(1/4)[3^(n+1) +(−1)^n ]](https://www.tinkutara.com/question/Q31998.png)
$${a}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{3}^{{n}+\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} \right] \\ $$
Commented by gunawan last updated on 18/Mar/18

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by prakash jain last updated on 18/Mar/18
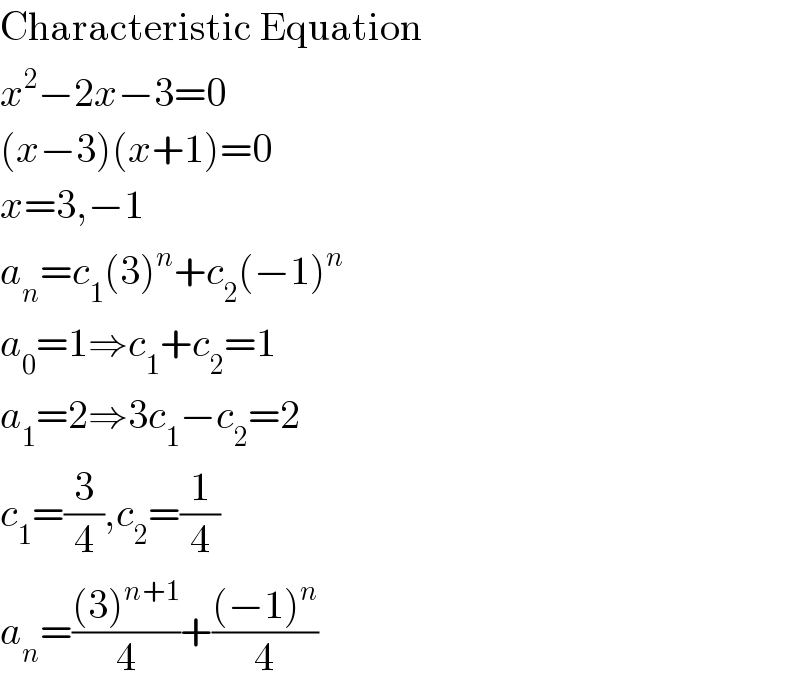
$$\mathrm{Characteristic}\:\mathrm{Equation} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{3},−\mathrm{1} \\ $$$${a}_{{n}} ={c}_{\mathrm{1}} \left(\mathrm{3}\right)^{{n}} +{c}_{\mathrm{2}} \left(−\mathrm{1}\right)^{{n}} \\ $$$${a}_{\mathrm{0}} =\mathrm{1}\Rightarrow{c}_{\mathrm{1}} +{c}_{\mathrm{2}} =\mathrm{1} \\ $$$${a}_{\mathrm{1}} =\mathrm{2}\Rightarrow\mathrm{3}{c}_{\mathrm{1}} −{c}_{\mathrm{2}} =\mathrm{2} \\ $$$${c}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{4}},{c}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${a}_{{n}} =\frac{\left(\mathrm{3}\right)^{{n}+\mathrm{1}} }{\mathrm{4}}+\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}} \\ $$
