Question Number 127226 by MathSh last updated on 27/Dec/20
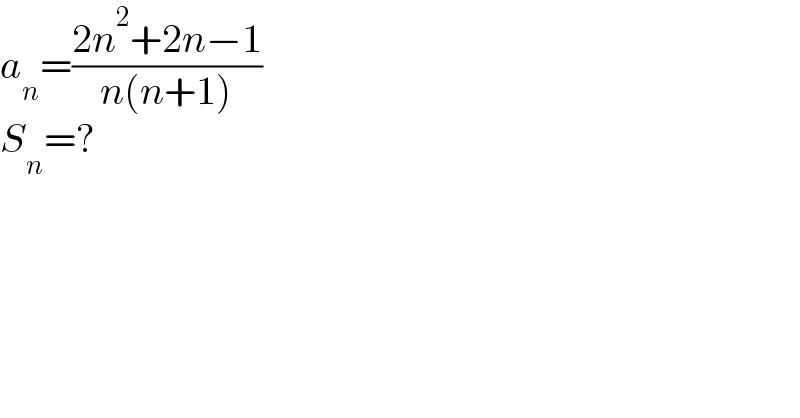
$${a}_{{n}} =\frac{\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}−\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)} \\ $$$${S}_{{n}} =? \\ $$
Answered by Ar Brandon last updated on 28/Dec/20
![a_n =((2n^2 +2n−1)/(n(n+1)))=((2n(n+1)−1)/(n(n+1))) =2−(1/(n(n+1)))=2−(1/n)+(1/(n+1)) S_n =2n+Σ_(k=1) ^n [(1/(k+1))−(1/k)]=2n+(−1+(1/(n+1)))](https://www.tinkutara.com/question/Q127227.png)
$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{2n}^{\mathrm{2}} +\mathrm{2n}−\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}=\frac{\mathrm{2n}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$\mathrm{S}_{\mathrm{n}} =\mathrm{2n}+\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{k}}\right]=\mathrm{2n}+\left(−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right) \\ $$
Commented by JDamian last updated on 27/Dec/20

$${Please},\:{rewrite}\:{the}\:{content}\:{inside}\:{the} \\ $$$${square}\:{brackets}\:{with}\:{the}\:{right}\:{ind}\mathrm{ex}\:\boldsymbol{\mathrm{k}}. \\ $$
