Question Number 98557 by M±th+et+s last updated on 14/Jun/20
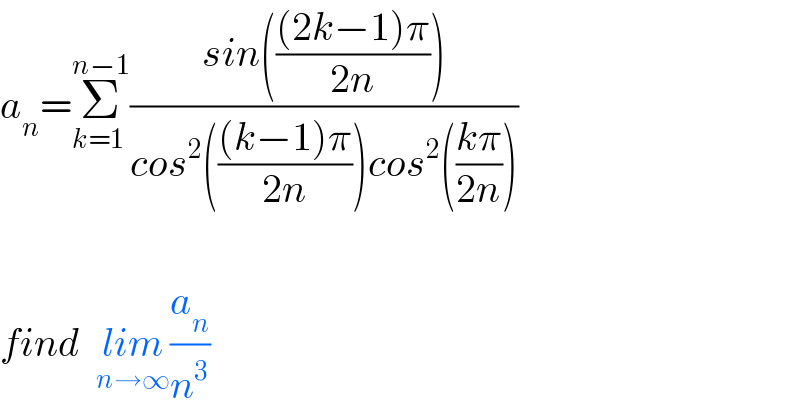
$${a}_{{n}} =\underset{{k}=\mathrm{1}\:} {\overset{{n}−\mathrm{1}} {\sum}}\frac{{sin}\left(\frac{\left(\mathrm{2}{k}−\mathrm{1}\right)\pi}{\mathrm{2}{n}}\right)}{{cos}^{\mathrm{2}} \left(\frac{\left({k}−\mathrm{1}\right)\pi}{\mathrm{2}{n}}\right){cos}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{2}{n}}\right)} \\ $$$$ \\ $$$${find}\:\:\underset{{n}\rightarrow\infty} {{lim}}\frac{{a}_{{n}} }{{n}^{\mathrm{3}} } \\ $$
