Question Number 24022 by Tinkutara last updated on 11/Nov/17

$$\mathrm{A}\:\mathrm{one}\:\mathrm{kg}\:\mathrm{ball}\:\mathrm{rolling}\:\mathrm{on}\:\mathrm{a}\:\mathrm{smooth} \\ $$$$\mathrm{horizontal}\:\mathrm{surface}\:\mathrm{at}\:\mathrm{20}\:\mathrm{m}\:\mathrm{s}^{−\mathrm{1}} \:\mathrm{comes}\:\mathrm{to} \\ $$$$\mathrm{the}\:\mathrm{bottom}\:\mathrm{of}\:\mathrm{an}\:\mathrm{inclined}\:\mathrm{plane}\:\mathrm{making} \\ $$$$\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{30}°\:\mathrm{with}\:\mathrm{the}\:\mathrm{horizontal}. \\ $$$$\mathrm{Calculate}\:\mathrm{K}.\mathrm{E}.\:\mathrm{of}\:\mathrm{the}\:\mathrm{ball}\:\mathrm{when}\:\mathrm{it}\:\mathrm{is}\:\mathrm{at} \\ $$$$\mathrm{the}\:\mathrm{bottom}\:\mathrm{of}\:\mathrm{incline}.\:\mathrm{How}\:\mathrm{far}\:\mathrm{up}\:\mathrm{the} \\ $$$$\mathrm{incline}\:\mathrm{will}\:\mathrm{the}\:\mathrm{ball}\:\mathrm{roll}?\:\mathrm{Neglect} \\ $$$$\mathrm{friction}. \\ $$
Answered by mrW1 last updated on 12/Nov/17
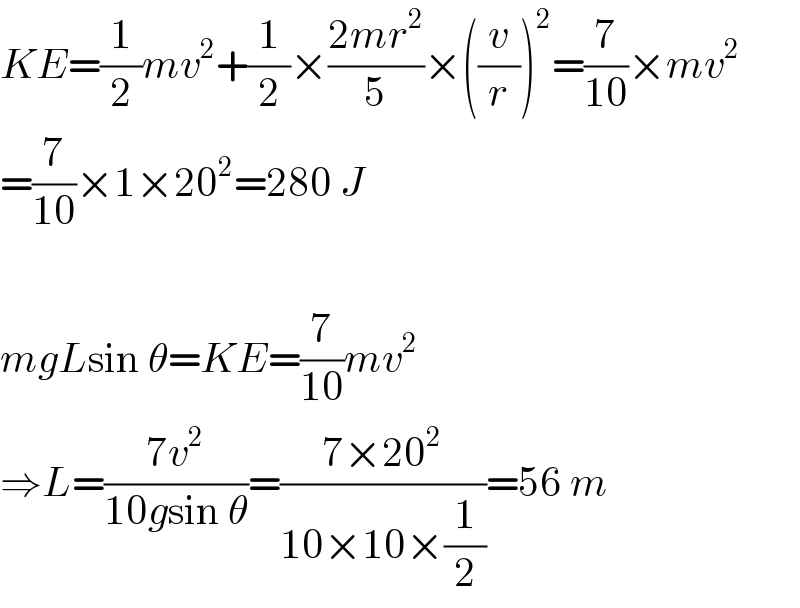
$${KE}=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{mr}^{\mathrm{2}} }{\mathrm{5}}×\left(\frac{{v}}{{r}}\right)^{\mathrm{2}} =\frac{\mathrm{7}}{\mathrm{10}}×{mv}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{7}}{\mathrm{10}}×\mathrm{1}×\mathrm{20}^{\mathrm{2}} =\mathrm{280}\:{J} \\ $$$$ \\ $$$${mgL}\mathrm{sin}\:\theta={KE}=\frac{\mathrm{7}}{\mathrm{10}}{mv}^{\mathrm{2}} \\ $$$$\Rightarrow{L}=\frac{\mathrm{7}{v}^{\mathrm{2}} }{\mathrm{10}{g}\mathrm{sin}\:\theta}=\frac{\mathrm{7}×\mathrm{20}^{\mathrm{2}} }{\mathrm{10}×\mathrm{10}×\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{56}\:{m} \\ $$
Commented by Tinkutara last updated on 12/Nov/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
