Menu Close

A-palindrome-is-a-number-that-remains-the-same-when-its-numbers-are-reversed-The-number-n-and-n-192-are-three-digit-and-four-digit-palindromes-respectively-What-is-the-sum-of-the-digits-of-m-Can-

Tinku Tara 0 Comments
Pin




Question Number 110587 by Aina Samuel Temidayo last updated on 29/Aug/20
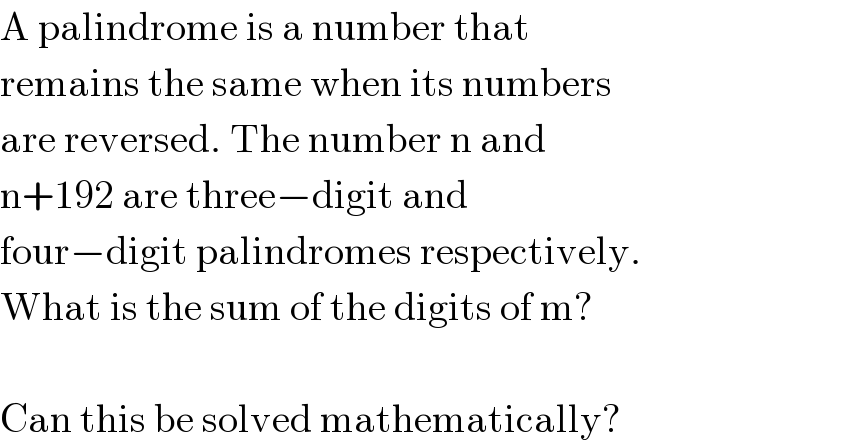
A palindrome is a number that remains the same when its numbers are reversed. The number n and n+192 are three−digit and four−digit palindromes respectively. What is the sum of the digits of m? Can this be solved mathematically?
$$\mathrm{A}\:\mathrm{palindrome}\:\mathrm{is}\:\mathrm{a}\:\mathrm{number}\:\mathrm{that} \\ $$$$\mathrm{remains}\:\mathrm{the}\:\mathrm{same}\:\mathrm{when}\:\mathrm{its}\:\mathrm{numbers} \\ $$$$\mathrm{are}\:\mathrm{reversed}.\:\mathrm{The}\:\mathrm{number}\:\mathrm{n}\:\mathrm{and} \\ $$$$\mathrm{n}+\mathrm{192}\:\mathrm{are}\:\mathrm{three}−\mathrm{digit}\:\mathrm{and} \\ $$$$\mathrm{four}−\mathrm{digit}\:\mathrm{palindromes}\:\mathrm{respectively}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{digits}\:\mathrm{of}\:\mathrm{m}?\: \\ $$$$ \\ $$$$\mathrm{Can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{mathematically}? \\ $$
Answered by floor(10²Eta[1]) last updated on 29/Aug/20
we just need to get a 4 digit palindrome that when subtracted by 192 we get a palindrome with 3 digits the first 4 digits palindromes are: 1001 1111 1221 .... notice that we can stop here because if we subtract 192 of 1221 we dont get a 3 digit number. now we just need to test those 2 cases: 1001−192=809. not a palindrome. 1111−192=919. is a palindrome so n=919 and the sum of the digits is 9+1+9=19
$$\mathrm{we}\:\mathrm{just}\:\mathrm{need}\:\mathrm{to}\:\mathrm{get}\:\mathrm{a}\:\mathrm{4}\:\mathrm{digit}\:\mathrm{palindrome} \\ $$$$\mathrm{that}\:\mathrm{when}\:\mathrm{subtracted}\:\mathrm{by}\:\mathrm{192}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\: \\ $$$$\mathrm{palindrome}\:\mathrm{with}\:\mathrm{3}\:\mathrm{digits} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{4}\:\mathrm{digits}\:\mathrm{palindromes}\:\mathrm{are}: \\ $$$$\mathrm{1001} \\ $$$$\mathrm{1111} \\ $$$$\mathrm{1221} \\ $$$$…. \\ $$$$\mathrm{notice}\:\mathrm{that}\:\mathrm{we}\:\mathrm{can}\:\mathrm{stop}\:\mathrm{here}\:\mathrm{because}\:\mathrm{if}\:\mathrm{we}\: \\ $$$$\mathrm{subtract}\:\mathrm{192}\:\mathrm{of}\:\mathrm{1221}\:\mathrm{we}\:\mathrm{dont}\:\mathrm{get}\:\mathrm{a}\: \\ $$$$\mathrm{3}\:\mathrm{digit}\:\mathrm{number}. \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{just}\:\mathrm{need}\:\mathrm{to}\:\mathrm{test}\:\mathrm{those}\:\mathrm{2}\:\mathrm{cases}: \\ $$$$\mathrm{1001}−\mathrm{192}=\mathrm{809}.\:\mathrm{not}\:\mathrm{a}\:\mathrm{palindrome}. \\ $$$$\mathrm{1111}−\mathrm{192}=\mathrm{919}.\:\mathrm{is}\:\mathrm{a}\:\mathrm{palindrome} \\ $$$$\mathrm{so}\:\mathrm{n}=\mathrm{919}\:\mathrm{and}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{digits} \\ $$$$\mathrm{is}\:\mathrm{9}+\mathrm{1}+\mathrm{9}=\mathrm{19} \\ $$
Commented by Aina Samuel Temidayo last updated on 29/Aug/20
Thanks.
$$\mathrm{Thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *