Question Number 114145 by ZiYangLee last updated on 17/Sep/20

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{moves}\:\mathrm{along}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\: \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{its}\:\mathrm{velocity},\:{v}\:\mathrm{m}\:\mathrm{s}^{−\mathrm{1}} ,\:\mathrm{is}\:\mathrm{given} \\ $$$$\mathrm{by}\:{v}={t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}{t},\:\mathrm{where}\:{t}\:\mathrm{is}\:\mathrm{time},\:\mathrm{in}\: \\ $$$$\mathrm{seconds},\:\mathrm{after}\:\mathrm{passing}\:\mathrm{through}\:\mathrm{fixed} \\ $$$$\mathrm{point}\:\mathrm{O}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{total}\:\mathrm{distance},\:\mathrm{in}\:\mathrm{m},\:\mathrm{travelled} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{until}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{returned} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{fixed}\:\mathrm{point}\:\mathrm{O}\:\mathrm{for}\:\mathrm{the}\:\mathrm{second}\:\mathrm{time}. \\ $$
Answered by mr W last updated on 17/Sep/20
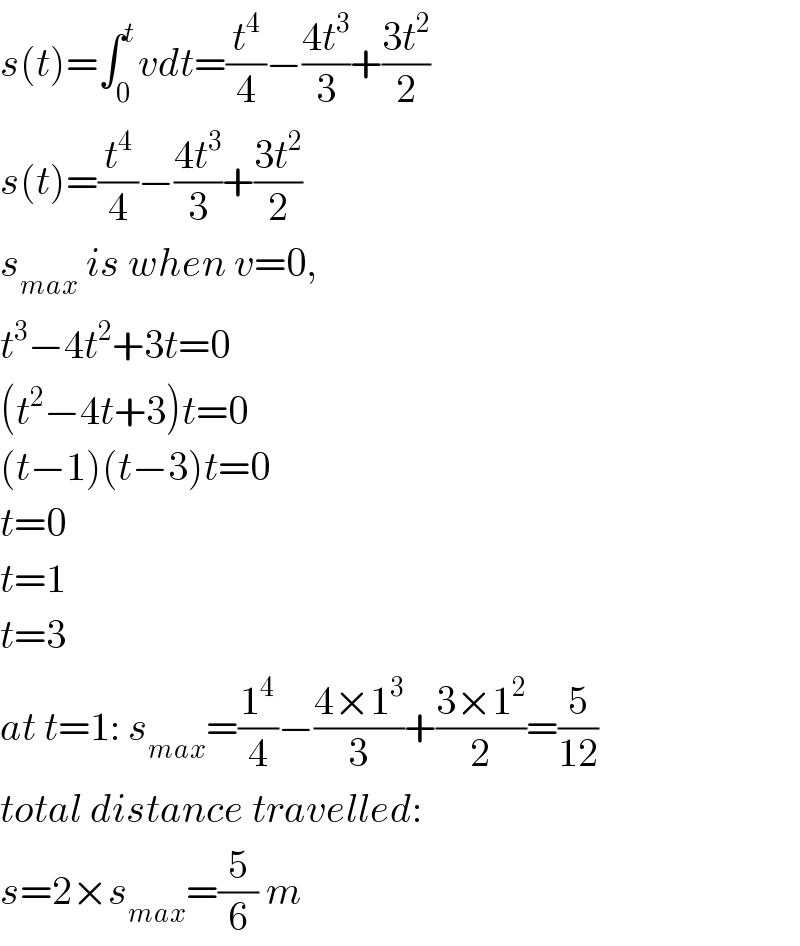
$${s}\left({t}\right)=\int_{\mathrm{0}} ^{{t}} {vdt}=\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{4}{t}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${s}\left({t}\right)=\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{4}{t}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${s}_{{max}} \:{is}\:{when}\:{v}=\mathrm{0}, \\ $$$${t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}{t}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{3}\right){t}=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left({t}−\mathrm{3}\right){t}=\mathrm{0} \\ $$$${t}=\mathrm{0} \\ $$$${t}=\mathrm{1} \\ $$$${t}=\mathrm{3} \\ $$$${at}\:{t}=\mathrm{1}:\:{s}_{{max}} =\frac{\mathrm{1}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{4}×\mathrm{1}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}×\mathrm{1}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{12}} \\ $$$${total}\:{distance}\:{travelled}: \\ $$$${s}=\mathrm{2}×{s}_{{max}} =\frac{\mathrm{5}}{\mathrm{6}}\:{m} \\ $$
Commented by ZiYangLee last updated on 17/Sep/20
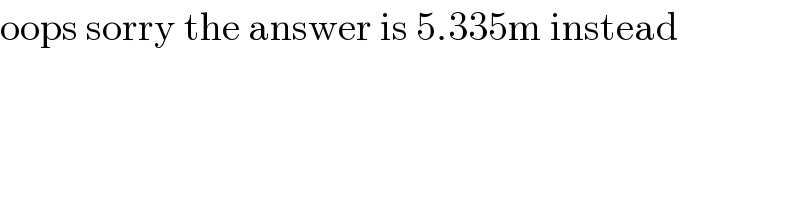
$$\mathrm{oops}\:\mathrm{sorry}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{5}.\mathrm{335m}\:\mathrm{instead} \\ $$
Commented by mr W last updated on 17/Sep/20

$${it}'{s}\:{upon}\:{what}\:{is}\:{meant}\:{with}\:“{return} \\ $$$${to}\:{point}\:{O}\:{for}\:{the}\:{second}\:{time}''. \\ $$$${what}\:{i}\:{meant}\:{is}\:{that}\:{the}\:{object}\:{leaves} \\ $$$${point}\:{O}\:{and}\:{comes}\:{back}.\:{but}\:{if}\:{it} \\ $$$${means}\:{that}\:{the}\:{object}\:{leaves}\:{point}\:{O} \\ $$$${and}\:{comes}\:{back}\:{and}\:{leaves}\:{again}\:{and} \\ $$$${comes}\:{back}\:{again},\:{then}\:{the}\:{result}\:{is}: \\ $$$${at}\:{t}=\mathrm{3}:\:{s}_{{min}} =\frac{\mathrm{3}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{4}×\mathrm{3}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}×\mathrm{3}^{\mathrm{2}} }{\mathrm{2}}=−\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$ \\ $$$$\Rightarrow{total}\:{distance}\:{moved}: \\ $$$$\mathrm{2}×\frac{\mathrm{5}}{\mathrm{12}}+\mathrm{2}×\frac{\mathrm{9}}{\mathrm{4}}=\frac{\mathrm{16}}{\mathrm{3}}=\mathrm{5}.\mathrm{333}\:{m} \\ $$
Commented by mr W last updated on 17/Sep/20

