A-particle-moves-in-a-linear-scare-such-that-acceleration-after-t-seconds-is-a-ms-2-where-a-2t-2-t-If-its-initial-velocity-was-3ms-1-find-an-expression-for-S-the-distance-in-meters-travele

FacebookTweetPin

Question Number 47967 by Rio Michael last updated on 17/Nov/18

$$Aparticlemovesinalinearscaresuchthatacceleration$$$$aftertsecondsisa{ms}^{-2}wherea=2t^2+t.Ifitsinitial$$$$velocitywas3{ms}^{-1}findanexpressionforS,thedistanceinmeters$$$$traveledfromstarttseconds.$$

Answered by ajfour last updated on 17/Nov/18

$$a=\frac{dv}{dt}=2t^2+t$$$$\Rightarrow {\int }_3^{v}dv={\int }_0^t(2t^2+t)dt$$$$\Rightarrow v=\frac{dx}{dt}=\frac{2}{3}{t}^3+\frac{t^2}{2}+3$$$$\Rightarrow {\int }_{x_9}^{x}dx={\int }_0^t(\frac{2}{3}{t}^3+\frac{t^2}{2}+3)dt$$$$s=x-x_0=t(\frac{t^3}{6}+\frac{t^2}{6}+3)$$$$\Rightarrow \text{boldsymbol}s=\frac{\text{boldsymbol}t}{6}(\text{boldsymbol}{t}^3+\text{boldsymbol}{t}^2+18).$$

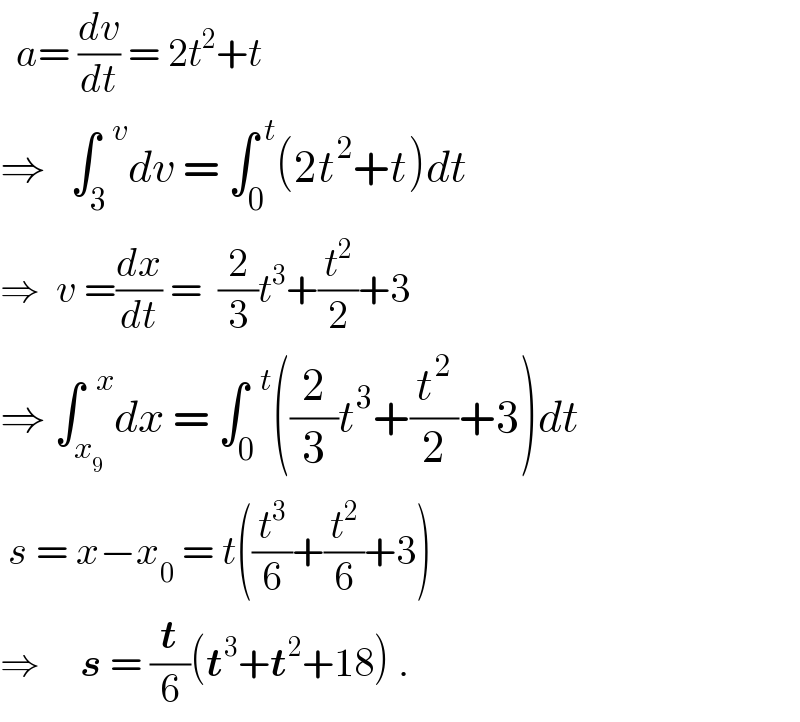
Commented by Rio Michael last updated on 17/Nov/18

$$pleasesiri{don}^{\prime }tunderstandthepointwhere$$$${\int }_{x_9}^{x}dx={\int }_0^t(\frac{2}{3}{t}^3+\frac{t^2}{2}+3)dt$$

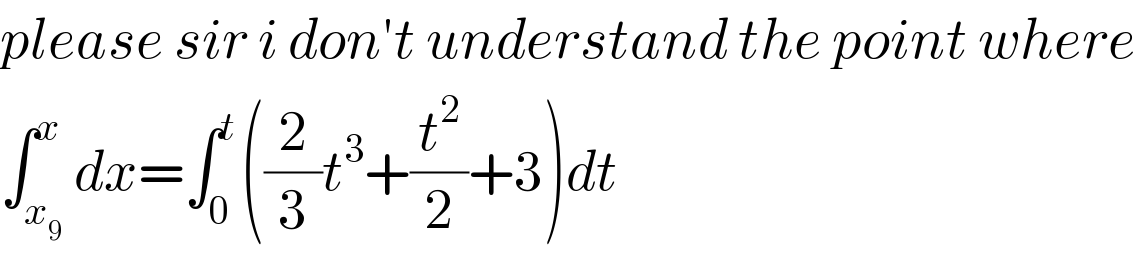
Commented by ajfour last updated on 17/Nov/18

$$xisthepositioncoordinate$$$$attimet,x_{0}theinitialposition$$$$coordinate;sthedisplacement$$$$isalways=△x=x-x_0.$$

Commented by Rio Michael last updated on 18/Nov/18

$$thankssir$$$$thankssir$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin