Question Number 54578 by pieroo last updated on 07/Feb/19
![A particle of mass 1.5kg rests on a rough plane inclined at 45° to the horizontal. It is maintained in equilibrium by a horizontal force of p newtons. Given that the coefficient of friction between the particle and the plane is (1/4), calculate the value of p when the particle is on the point of moving i. down the plane ii. up the plane [take g=10ms^(−2) ].](https://www.tinkutara.com/question/Q54578.png)
Commented by pieroo last updated on 07/Feb/19

Answered by mr W last updated on 07/Feb/19
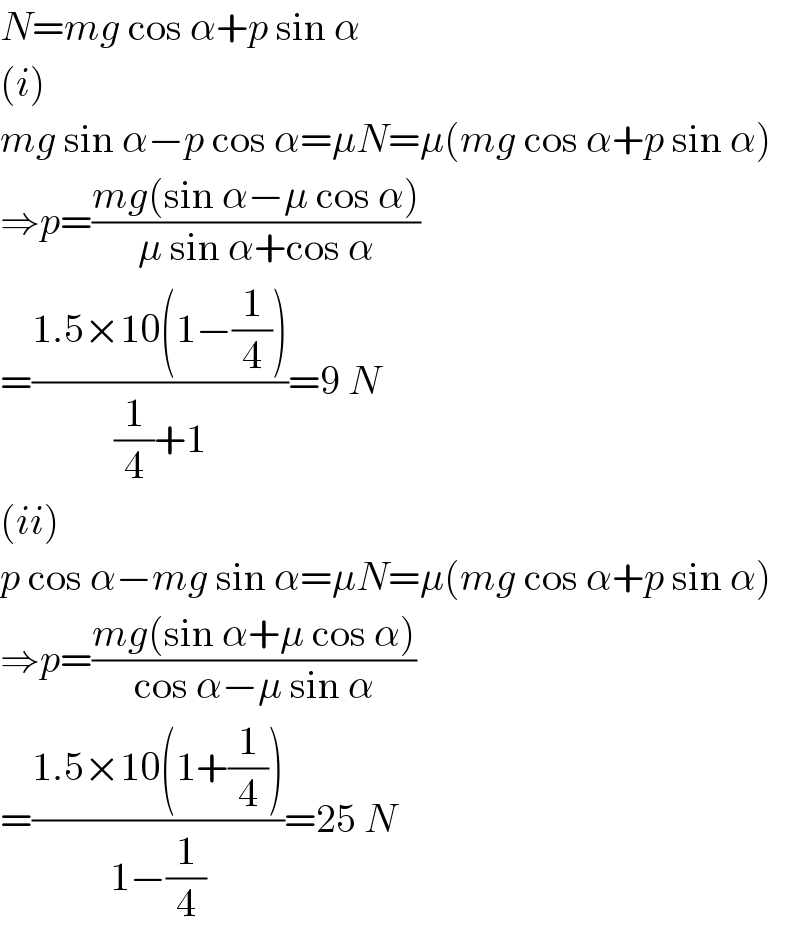
Commented by mr W last updated on 07/Feb/19
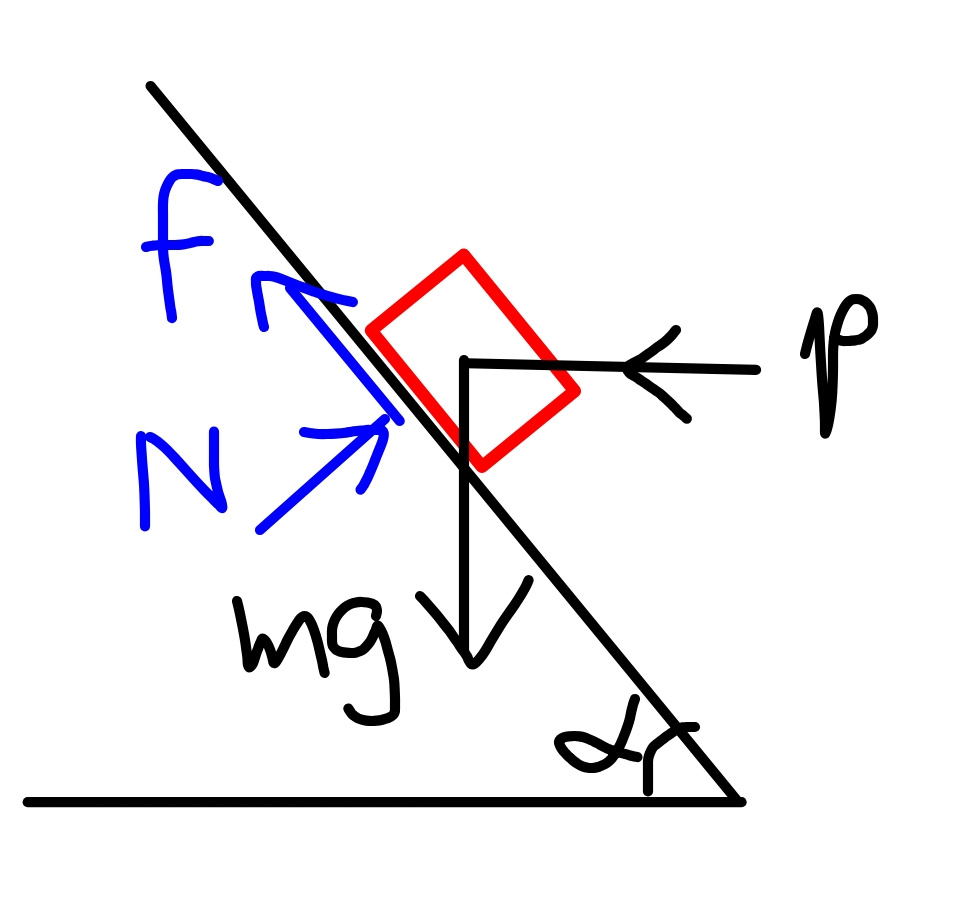
Commented by mr W last updated on 07/Feb/19
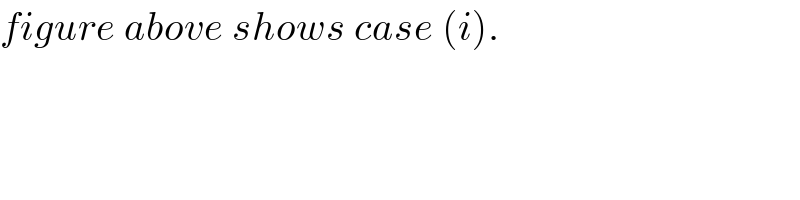
Commented by pieroo last updated on 08/Feb/19

