A-particle-of-mass-500g-is-placed-on-a-plane-inclined-at-an-angle-30-to-the-horizontal-What-force-is-i-acting-parallel-to-the-plane-ii-acting-horizontally-is-required-to-hold-the-particle-at-re

FacebookTweetPin

Question Number 111282 by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{A}\mathrm{particle}\mathrm{of}\mathrm{mass}500\mathrm{g}\mathrm{is}\mathrm{placed}\mathrm{on}\mathrm{a}$$$$\mathrm{plane}\mathrm{inclined}\mathrm{at}\mathrm{an}\mathrm{angle}30°$$$$\mathrm{to}\mathrm{the}\mathrm{horizontal}.\mathrm{What}\mathrm{force}\mathrm{is}$$$$\left(\mathrm{i}\right)\mathrm{acting}\mathrm{parallel}\mathrm{to}\mathrm{the}\mathrm{plane}$$$$\left(\mathrm{ii}\right)\mathrm{acting}\mathrm{horizontally}\mathrm{is}\mathrm{required}\mathrm{to}$$$$\mathrm{hold}\mathrm{the}\mathrm{particle}\mathrm{at}\mathrm{rest}(\mathrm{g}=10\mathrm{m}/{\mathrm{s}}^2)$$

Answered by ajfour last updated on 03/Sep/20

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Solution}\mathrm{please}?$$

Commented by ajfour last updated on 03/Sep/20

$$\left(i\right)F=mg\sin 30°$$$$=\frac{1}{2}\times 10\times \frac{1}{2}=2.5N$$$$\left(ii\right)F=N\sin 30°$$$$N\cos 30°=mg=\frac{1}{2}\times 10=5$$$$\Rightarrow F=\frac{5}{\cos 30°}\times \sin 30°=\frac{5}{\sqrt{3}}newtons.$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Kindly}\mathrm{explain}\mathrm{no}.2\mathrm{in}\mathrm{details}\mathrm{please}.$$$$\mathrm{Thanks}.$$

Commented by ajfour last updated on 03/Sep/20

$$forcebalancealongverticaland$$$$horizontalgives:$$$$N\cos 30°=mg$$$$N\sin 30°=F$$$$dividing$$$$\frac{F}{mg}=\tan 30°=\frac{1}{\sqrt{3}}$$$$\Rightarrow F=\frac{mg}{\sqrt{3}}=\frac{\left(1/2\right)\times 10}{\sqrt{3}}=\frac{5}{\sqrt{3}}=\frac{5\sqrt{3}}{3}.$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{I}{\mathrm{don}}^{\prime }\mathrm{t}\mathrm{really}\mathrm{understand}\mathrm{the}\mathrm{diagram}$$$$\mathrm{for}\left(\mathrm{ii}\right)$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Is}\mathrm{that}\mathrm{the}\mathrm{correct}\mathrm{position}\mathrm{for}\mathrm{F}?$$

Commented by ajfour last updated on 03/Sep/20

$$yes{it}^{\prime }llbelike{i}^{\prime }vedrawn.$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Why}\mathrm{is}\mathrm{that}\mathrm{so}?$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

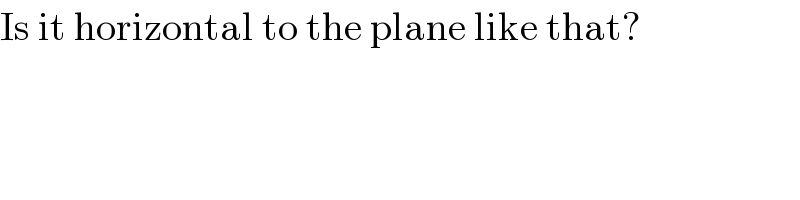
$$\mathrm{Is}\mathrm{it}\mathrm{horizontal}\mathrm{to}\mathrm{the}\mathrm{plane}\mathrm{like}\mathrm{that}?$$

Commented by ajfour last updated on 03/Sep/20

$$yestheforcethatishorizontal$$$$andneededtoholdtheparticle$$$$againstthefrictionlessincline$$$$willbedirectedsuchwiseand$$$$F=mg\tan \theta .$$$$horizontalmeansparalleltoflat$$$$ground,youshouldnotsayhorizontal$$$$toplane\left(inclined\right)!$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{What}\mathrm{about}\mathrm{the}\mathrm{dotted}\mathrm{line}\mathrm{opposite}$$$$\mathrm{to}\mathrm{it}?$$

Commented by ajfour last updated on 03/Sep/20

$$thecomponentofNormalreaction$$$$alongthatdottedlineisN\sin 30°$$$$whichthehorizontalforcwFis$$$$balancing.$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{So}\mathrm{which}\mathrm{angle}\mathrm{are}\mathrm{we}\mathrm{using}?$$

Commented by ajfour last updated on 03/Sep/20

Commented by ajfour last updated on 03/Sep/20

$$N\cos (90°-30°)=F$$$$\Rightarrow N\sin 30°=F$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{How}\mathrm{did}\mathrm{you}\mathrm{get}\mathrm{that}30°\mathrm{close}\mathrm{to}\mathrm{N}?$$

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{I}\mathrm{think}\mathrm{I}\mathrm{understand}\mathrm{now}.\mathrm{Thanks}.$$

Commented by ajfour last updated on 03/Sep/20

Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Yes}.\mathrm{Thanks}\mathrm{for}\mathrm{your}\mathrm{time}.\mathrm{I}\mathrm{really}$$$$\mathrm{appreciate}\mathrm{your}\mathrm{efforts}.$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin