A-particle-s-trajectory-is-described-by-x-e-t-e-t-y-2t-Find-the-distance-that-the-particle-traveled-for-0-t-2-

Question Number 103400 by abony1303 last updated on 14/Jul/20

$$\mathrm{A}\:\mathrm{particle}'\mathrm{s}\:\mathrm{trajectory}\:\mathrm{is}\:\mathrm{described}\:\mathrm{by} \\ $$$$\mathrm{x}=\mathrm{e}^{\mathrm{t}} +\mathrm{e}^{−\mathrm{t}} \:\:\:\:\:\mathrm{y}=\mathrm{2t} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{that}\:\mathrm{the}\:\mathrm{particle} \\ $$$$\mathrm{traveled}\:\mathrm{for}\:\mathrm{0}\leqslant\mathrm{t}\leqslant\mathrm{2} \\ $$

Commented by abony1303 last updated on 14/Jul/20

$$\mathrm{Pls}\:\mathrm{help} \\ $$

Answered by mr W last updated on 14/Jul/20

dx=(e^t −e^(−t) )dt dy=2dt ds=(√((dx)^2 +(dy)^2 ))=(√((e^t −e^(−t) )^2 +4)) dt =(e^t +e^(−t) )dt s(t)=∫_0 ^t ds=∫_0 ^t (e^t +e^(−t) )dt=[e^t −e^(−t) ]_0 ^t =e^t −e^(−t) ⇒s(2)=e^2 −(1/e^2 )

$${dx}=\left({e}^{{t}} −{e}^{−{t}} \right){dt} \\ $$$${dy}=\mathrm{2}{dt} \\ $$$${ds}=\sqrt{\left({dx}\right)^{\mathrm{2}} +\left({dy}\right)^{\mathrm{2}} }=\sqrt{\left({e}^{{t}} −{e}^{−{t}} \right)^{\mathrm{2}} +\mathrm{4}}\:{dt} \\ $$$$=\left({e}^{{t}} +{e}^{−{t}} \right){dt} \\ $$$${s}\left({t}\right)=\int_{\mathrm{0}} ^{{t}} {ds}=\int_{\mathrm{0}} ^{{t}} \left({e}^{{t}} +{e}^{−{t}} \right){dt}=\left[{e}^{{t}} −{e}^{−{t}} \right]_{\mathrm{0}} ^{{t}} \\ $$$$={e}^{{t}} −{e}^{−{t}} \\ $$$$\Rightarrow{s}\left(\mathrm{2}\right)={e}^{\mathrm{2}} −\frac{\mathrm{1}}{{e}^{\mathrm{2}} } \\ $$

Commented by abony1303 last updated on 14/Jul/20

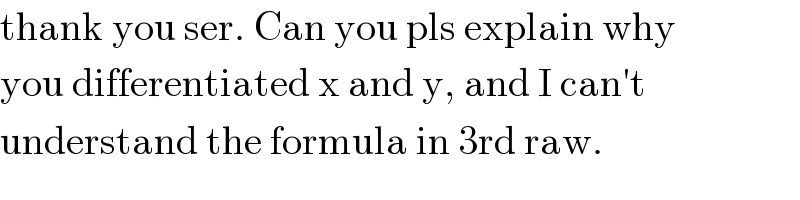
thank you ser. Can you pls explain why you differentiated x and y, and I can′t understand the formula in 3rd raw.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{ser}.\:\mathrm{Can}\:\mathrm{you}\:\mathrm{pls}\:\mathrm{explain}\:\mathrm{why}\: \\ $$$$\mathrm{you}\:\mathrm{differentiated}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y},\:\mathrm{and}\:\mathrm{I}\:\mathrm{can}'\mathrm{t} \\ $$$$\mathrm{understand}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{in}\:\mathrm{3rd}\:\mathrm{raw}. \\ $$

Commented by mr W last updated on 14/Jul/20

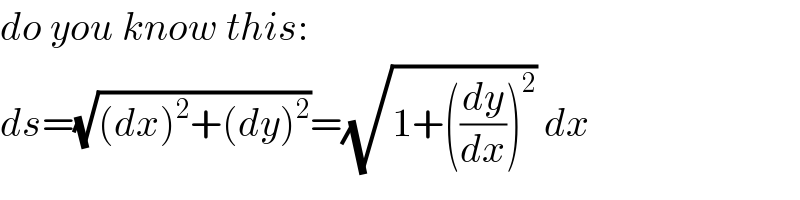
do you know this: ds=(√((dx)^2 +(dy)^2 ))=(√(1+((dy/dx))^2 )) dx

$${do}\:{you}\:{know}\:{this}: \\ $$$${ds}=\sqrt{\left({dx}\right)^{\mathrm{2}} +\left({dy}\right)^{\mathrm{2}} }=\sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} }\:{dx} \\ $$

Commented by mr W last updated on 14/Jul/20

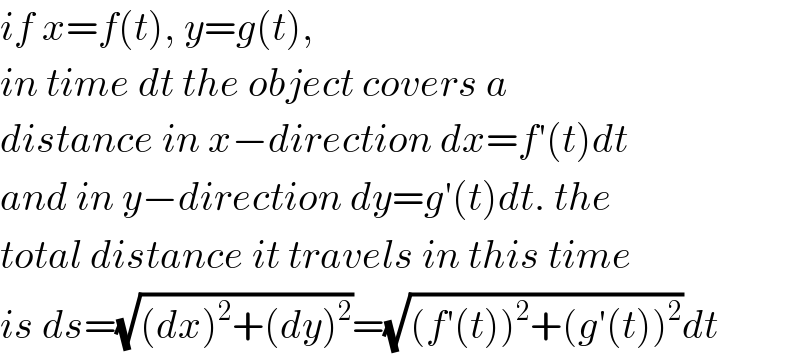
if x=f(t), y=g(t), in time dt the object covers a distance in x−direction dx=f′(t)dt and in y−direction dy=g′(t)dt. the total distance it travels in this time is ds=(√((dx)^2 +(dy)^2 ))=(√((f′(t))^2 +(g′(t))^2 ))dt

$${if}\:{x}={f}\left({t}\right),\:{y}={g}\left({t}\right), \\ $$$${in}\:{time}\:{dt}\:{the}\:{object}\:{covers}\:{a} \\ $$$${distance}\:{in}\:{x}−{direction}\:{dx}={f}'\left({t}\right){dt} \\ $$$${and}\:{in}\:{y}−{direction}\:{dy}={g}'\left({t}\right){dt}.\:{the} \\ $$$${total}\:{distance}\:{it}\:{travels}\:{in}\:{this}\:{time} \\ $$$${is}\:{ds}=\sqrt{\left({dx}\right)^{\mathrm{2}} +\left({dy}\right)^{\mathrm{2}} }=\sqrt{\left({f}'\left({t}\right)\right)^{\mathrm{2}} +\left({g}'\left({t}\right)\right)^{\mathrm{2}} }{dt} \\ $$

Answered by OlafThorendsen last updated on 14/Jul/20

0≤t≤2 ⇔ 0≤y≤4 x = e^t +e^(−t) = 2cht = 2ch(y/2) (dx/dy) = 2×(1/2)sh(y/2) = sh(y/2) d = ∫_0 ^4 (√(1+((dx/dy))^2 ))dy d = ∫_0 ^4 (√(1+sh^2 (y/2)))dy d = ∫_0 ^4 ch(y/2)dy d = [2sh(y/2)]_0 ^4 = 2sh2 = e^2 −(1/e^2 )

$$\mathrm{0}\leqslant{t}\leqslant\mathrm{2}\:\Leftrightarrow\:\mathrm{0}\leqslant{y}\leqslant\mathrm{4} \\ $$$${x}\:=\:{e}^{{t}} +{e}^{−{t}} \:=\:\mathrm{2ch}{t}\:=\:\mathrm{2ch}\frac{{y}}{\mathrm{2}} \\ $$$$\frac{{dx}}{{dy}}\:=\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}\frac{{y}}{\mathrm{2}}\:=\:\mathrm{sh}\frac{{y}}{\mathrm{2}} \\ $$$$\mathrm{d}\:=\:\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{\mathrm{1}+\left(\frac{{dx}}{{dy}}\right)^{\mathrm{2}} }{dy} \\ $$$$\mathrm{d}\:=\:\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{\mathrm{1}+\mathrm{sh}^{\mathrm{2}} \frac{{y}}{\mathrm{2}}}{dy} \\ $$$$\mathrm{d}\:=\:\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{ch}\frac{{y}}{\mathrm{2}}{dy} \\ $$$$\mathrm{d}\:=\:\left[\mathrm{2sh}\frac{{y}}{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{4}} \:=\:\mathrm{2sh2}\:=\:{e}^{\mathrm{2}} −\frac{\mathrm{1}}{{e}^{\mathrm{2}} } \\ $$

Answered by Dwaipayan Shikari last updated on 14/Jul/20

(dx/dt)=e^t −e^(−t) (dy/dt)=2 Resultant =(√(△x^2 +△y^2 ))=(√((e^t −e^(−t) )^2 +4 ))=e^t +e^(−t) Time is bounded (0,2) ∫_0 ^2 e^t −e^(−t) dt=e^2 −(1/e^2 ) (Resultant tracetory)

$$\frac{{dx}}{{dt}}={e}^{{t}} −{e}^{−{t}} \\ $$$$\frac{{dy}}{{dt}}=\mathrm{2} \\ $$$${Resultant}\:=\sqrt{\bigtriangleup{x}^{\mathrm{2}} +\bigtriangleup{y}^{\mathrm{2}} }=\sqrt{\left({e}^{{t}} −{e}^{−{t}} \right)^{\mathrm{2}} +\mathrm{4}\:\:}={e}^{{t}} +{e}^{−{t}} \\ $$$${Time}\:{is}\:{bounded}\:\left(\mathrm{0},\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} {e}^{{t}} −{e}^{−{t}} {dt}={e}^{\mathrm{2}} −\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\:\:\:\left({Resultant}\:{tracetory}\right) \\ $$

Facebook Tweet Pin

A-particle-s-trajectory-is-described-by-x-e-t-e-t-y-2t-Find-the-distance-that-the-particle-traveled-for-0-t-2-

Leave a Reply Cancel reply