Question Number 170202 by otchereabdullai@gmail.com last updated on 18/May/22

Commented by otchereabdullai@gmail.com last updated on 18/May/22
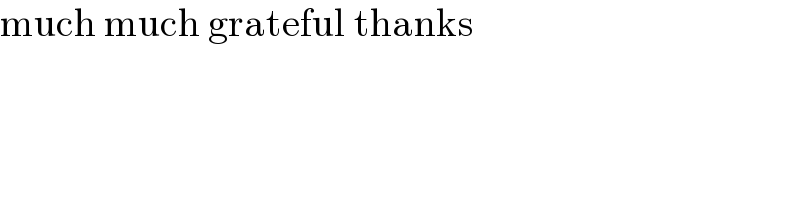
Commented by mr W last updated on 18/May/22
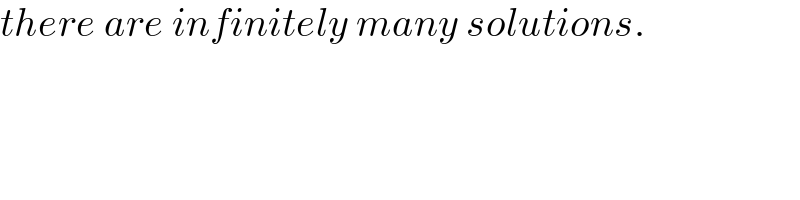
Commented by MJS_new last updated on 18/May/22
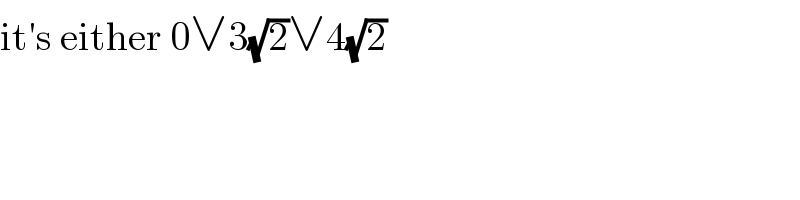
Commented by otchereabdullai@gmail.com last updated on 18/May/22
Commented by otchereabdullai@gmail.com last updated on 18/May/22
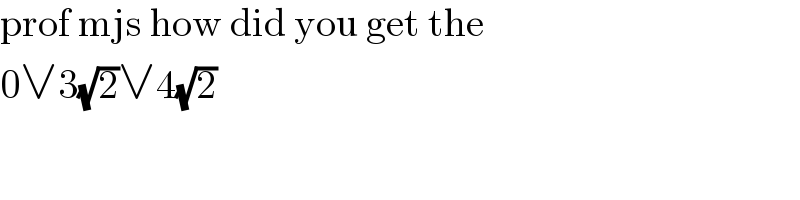
Commented by MJS_new last updated on 18/May/22

Commented by mr W last updated on 18/May/22
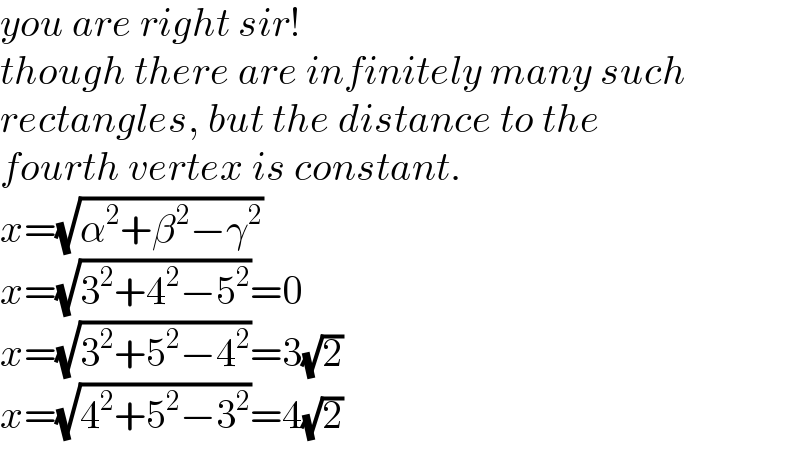
Commented by mr W last updated on 18/May/22
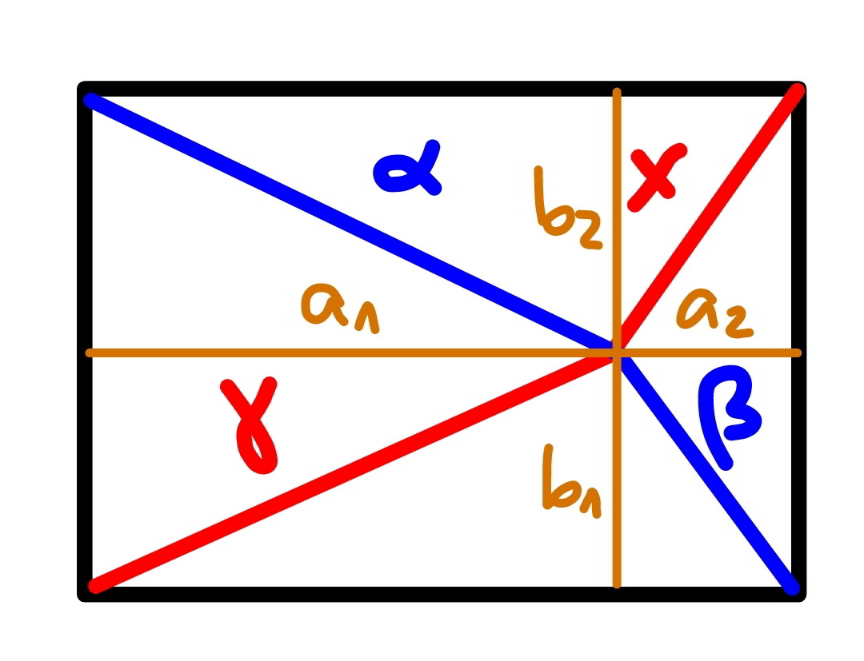
Commented by mr W last updated on 18/May/22
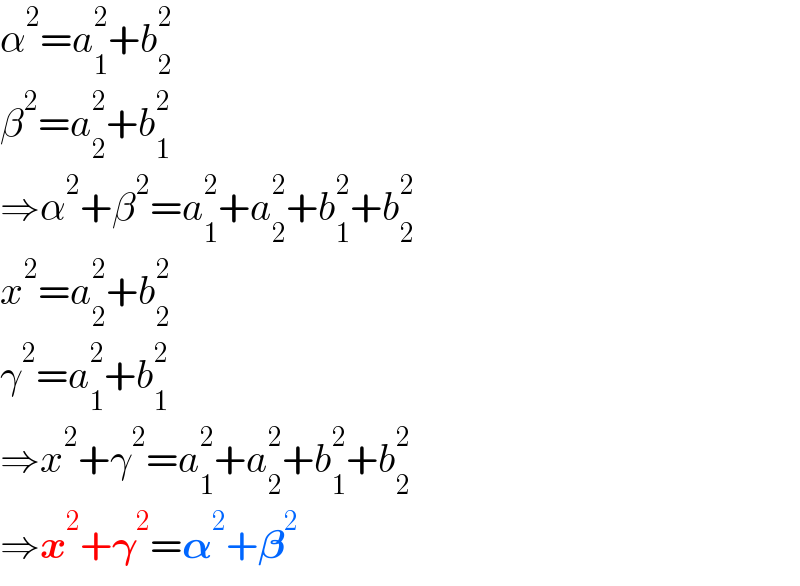
Commented by Tawa11 last updated on 08/Oct/22

