A-polynomial-f-x-with-rational-coefficients-leaves-remainder-15-when-divided-by-x-3-and-remainder-2x-1-when-divided-by-x-1-2-Find-the-remainder-when-f-x-is-divided-by-x-3-x-1-2-

Question Number 19101 by Tinkutara last updated on 04/Aug/17

$$\mathrm{A}\:\mathrm{polynomial}\:{f}\left({x}\right)\:\mathrm{with}\:\mathrm{rational} \\ $$$$\mathrm{coefficients}\:\mathrm{leaves}\:\mathrm{remainder}\:\mathrm{15},\:\mathrm{when} \\ $$$$\mathrm{divided}\:\mathrm{by}\:{x}\:−\:\mathrm{3}\:\mathrm{and}\:\mathrm{remainder}\:\mathrm{2}{x}\:+\:\mathrm{1}, \\ $$$$\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} .\:\mathrm{Find}\:\mathrm{the} \\ $$$$\mathrm{remainder}\:\mathrm{when}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by} \\ $$$$\left({x}\:−\:\mathrm{3}\right)\left({x}\:−\:\mathrm{1}\right)^{\mathrm{2}} . \\ $$

Commented by prakash jain last updated on 04/Aug/17

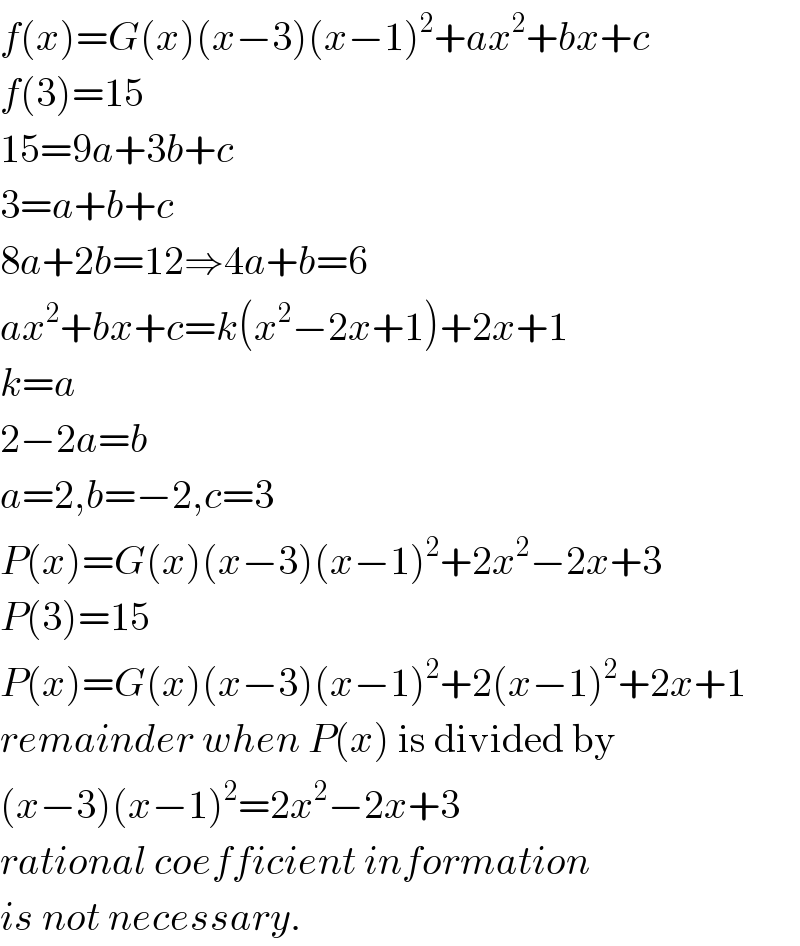
f(x)=G(x)(x−3)(x−1)^2 +ax^2 +bx+c f(3)=15 15=9a+3b+c 3=a+b+c 8a+2b=12⇒4a+b=6 ax^2 +bx+c=k(x^2 −2x+1)+2x+1 k=a 2−2a=b a=2,b=−2,c=3 P(x)=G(x)(x−3)(x−1)^2 +2x^2 −2x+3 P(3)=15 P(x)=G(x)(x−3)(x−1)^2 +2(x−1)^2 +2x+1 remainder when P(x) is divided by (x−3)(x−1)^2 =2x^2 −2x+3 rational coefficient information is not necessary.

$${f}\left({x}\right)={G}\left({x}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} +{ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{15} \\ $$$$\mathrm{15}=\mathrm{9}{a}+\mathrm{3}{b}+{c} \\ $$$$\mathrm{3}={a}+{b}+{c} \\ $$$$\mathrm{8}{a}+\mathrm{2}{b}=\mathrm{12}\Rightarrow\mathrm{4}{a}+{b}=\mathrm{6} \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}={k}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)+\mathrm{2}{x}+\mathrm{1} \\ $$$${k}={a} \\ $$$$\mathrm{2}−\mathrm{2}{a}={b} \\ $$$${a}=\mathrm{2},{b}=−\mathrm{2},{c}=\mathrm{3} \\ $$$${P}\left({x}\right)={G}\left({x}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3} \\ $$$${P}\left(\mathrm{3}\right)=\mathrm{15} \\ $$$${P}\left({x}\right)={G}\left({x}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$$${remainder}\:{when}\:{P}\left({x}\right)\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3} \\ $$$${rational}\:{coefficient}\:{information} \\ $$$${is}\:{not}\:{necessary}. \\ $$

Commented by RasheedSindhi last updated on 05/Aug/17

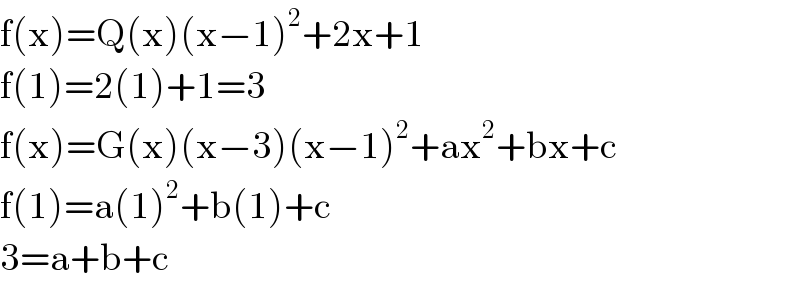
f(x)=Q(x)(x−1)^2 +2x+1 f(1)=2(1)+1=3 f(x)=G(x)(x−3)(x−1)^2 +ax^2 +bx+c f(1)=a(1)^2 +b(1)+c 3=a+b+c

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{Q}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2x}+\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{2}\left(\mathrm{1}\right)+\mathrm{1}=\mathrm{3} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{G}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{a}\left(\mathrm{1}\right)^{\mathrm{2}} +\mathrm{b}\left(\mathrm{1}\right)+\mathrm{c} \\ $$$$\mathrm{3}=\mathrm{a}+\mathrm{b}+\mathrm{c} \\ $$

Commented by Tinkutara last updated on 05/Aug/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Facebook Tweet Pin

A-polynomial-f-x-with-rational-coefficients-leaves-remainder-15-when-divided-by-x-3-and-remainder-2x-1-when-divided-by-x-1-2-Find-the-remainder-when-f-x-is-divided-by-x-3-x-1-2-

Leave a Reply Cancel reply