A-positive-number-has-8-distinct-divisors-Lets-say-a-b-c-d-e-f-g-and-h-Given-a-b-c-d-e-f-g-h-3111696-Find-that-number-

Question Number 27651 by Joel578 last updated on 12/Jan/18

A positive number has 8 distinct divisors

Lets say a, b, c, d, e, f, g and h

Given a . b . c . d . e . f . g . h = 3111696

Find that number

Commented by Joel578 last updated on 12/Jan/18

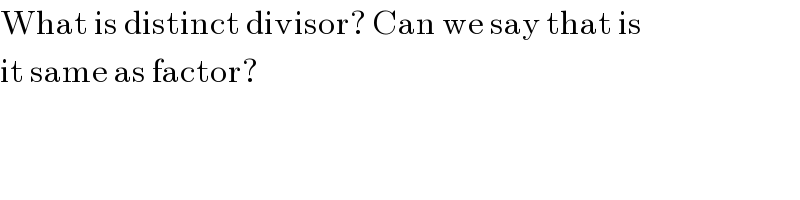
What is distinct divisor ? Can we say that is

it same as factor ?

Commented by Rasheed.Sindhi last updated on 14/Jan/18

Distinct divisors means differnt

divisors and yes divisor is same

as factor .

If a ∣ c & b ∣ c & a \neq b then a and b

are distinct divisors .

Answered by mrW2 last updated on 14/Jan/18

T h e n u m b e r i s 2 \times 3 \times 7 = 42 . I t h a s

e x a c t l y 8 (d i s t i n c t) d i v i s o r s :

1 (= a)

2 (= b)

3 (= c)

6 (= d)

7 (= e)

14 (= f)

21 (= g)

42 (= h)

T h e p r o d u c t o f a l l t h o s e d i v i s o r s i s

a \cdot b \cdot c \cdot d \cdot e \cdot f \cdot g \cdot h = 1 \times 2 \times 3 \times 6 \times 7 \times 14 \times 21 \times 42 = 311696

Commented by Rasheed.Sindhi last updated on 13/Jan/18

Hi Sir mrW 1 ∣ mrW 2

Your answer is perfect as it contains

all the divisors of required number .

I deleted my answer because its

logic was deffective .

Commented by mrW2 last updated on 13/Jan/18

S i r, t o b e h o n e s t, I {d i d n}^{'} t c a t c h t h e

q u e s t i o n r e a l l y t i l l I s a w y o u r w o r k i n g .

I t b r o u g h t m e f i n a l l y t o t h e r i g h t

u n d e r s t a n d i n g a n d t o t h e a n s w e r .

T h e r e f o r e t h a n k y o u f o r y o u r w o r k i n g!

Commented by Rasheed.Sindhi last updated on 13/Jan/18

T h A n K s S i R!

C ould Y ou H elp M e in solving

You can't use 'macro parameter character #' in math mode

Answered by mrW2 last updated on 14/Jan/18

A n o t h e r w a y t o s o l v e t h i s q u e s t i o n :

W e k n o w t h e n u m b e r, {l e t}^{'} s s a y N h a s

8 d i f f e r e n t d i v i s o r s a, b, c \dots, h .

W e k n o w i f n u m b e r k i s a d i v i s o r o f

N, t h e n \frac{N}{k} m u s t b e a n o t h e r d i v i s o r o f

i t, t h e p r o d u c t o f b o t h d i v i s o r s i s N .

T h i s i s t o s a y i f w e a r r a n g e a, b, c \dots, h

i n c r e a s i n g l y, {w e}^{'} l l h a v e

a \cdot h = N

b \cdot g = N

c \cdot f = N

d \cdot e = N

T h e n {w e}^{'} l l g e t

a \cdot b \cdot c \cdot d \cdot e \cdot f \cdot g \cdot h = N^{4} = 3111696 (a s g i v e n)

a c c o r d i n g t o S i r R a s h e e d . S i n d h i : 3111696 = {(2 \times 3 \times 7)}^{4}

\Rightarrow N = 2 \times 3 \times 7 = 42

Commented by Rasheed.Sindhi last updated on 14/Jan/18

C r e a t i v e w o r k S i r!

T h i s i s r e a l y a^{'} m e t h o d^{'} f o r

s u c h p r o b l e m s!

Commented by Joel578 last updated on 14/Jan/18

t h a n k y o u v e r y m u c h

Facebook Tweet Pin