Question Number 125052 by bramlexs22 last updated on 08/Dec/20

$$\:{A}\:{rescue}\:{cable}\:{attached}\:{to}\:{a}\: \\ $$$${helicopter}'{s}\:{weighs}\:\mathrm{2}\:{lb}/{ft}.\: \\ $$$${A}\:{man}\:\mathrm{180}−{lb}\:{grabs}\:{the}\:{end}\: \\ $$$${of}\:{the}\:{rope}\:{and}\:{his}\:{pulled}\: \\ $$$${from}\:{the}\:{ocean}\:{into}\:{the}\:{helicopter}. \\ $$$${How}\:{much}\:{work}\:{is}\:{done}\:{in}\: \\ $$$${lifting}\:{the}\:{man}\:{if}\:{the}\:{helicopter} \\ $$$${is}\:\mathrm{40}\:{ft}\:{above}\:{the}\:{water}\:? \\ $$$$\left({a}\right)\:\mathrm{8800}\:{lb}−{ft} \\ $$$$\left({b}\right)\:\mathrm{1780}\:{lb}−{ft} \\ $$$$\left({c}\right)\:\mathrm{7280}\:{lb}−{ft} \\ $$$$\left({d}\right)\:\mathrm{10},\mathrm{400}\:{lb}−{ft} \\ $$
Commented by mr W last updated on 08/Dec/20
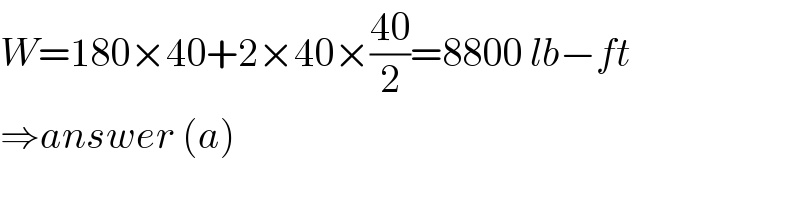
$${W}=\mathrm{180}×\mathrm{40}+\mathrm{2}×\mathrm{40}×\frac{\mathrm{40}}{\mathrm{2}}=\mathrm{8800}\:{lb}−{ft} \\ $$$$\Rightarrow{answer}\:\left({a}\right) \\ $$
Commented by benjo_mathlover last updated on 08/Dec/20
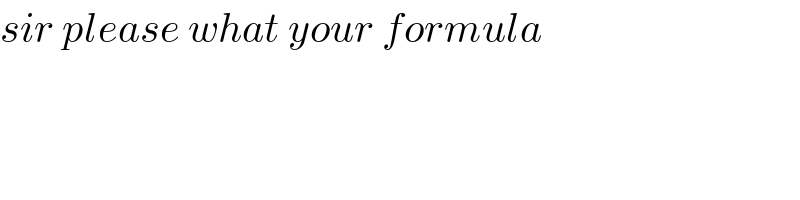
$${sir}\:{please}\:{what}\:{your}\:{formula} \\ $$
Commented by mr W last updated on 08/Dec/20

$${man}: \\ $$$${weight}\:=\mathrm{180}\:{lb} \\ $$$${distance}\:{moved}=\mathrm{40}\:{ft} \\ $$$${work}\:{done}=\mathrm{180}×\mathrm{40}\:{lb}−{ft} \\ $$$$ \\ $$$${rope}: \\ $$$${length}=\mathrm{40}{ft} \\ $$$${weight}=\mathrm{2}×\mathrm{40}\:{lb} \\ $$$${distance}\:{moved}=\frac{\mathrm{40}}{\mathrm{2}}\:{ft} \\ $$$$\left({center}\:{of}\:{mass}\:{of}\:{rope}\:{is}\:\frac{\mathrm{40}}{\mathrm{2}}\:{beneath}\right. \\ $$$$\left.{the}\:{helicopter}\right) \\ $$$${work}\:{done}=\mathrm{2}×\mathrm{40}×\frac{\mathrm{40}}{\mathrm{2}}\:{lb}−{ft} \\ $$
