Question Number 23066 by Tinkutara last updated on 25/Oct/17

Commented by Physics lover last updated on 26/Oct/17

Commented by math solver last updated on 26/Oct/17

Commented by Physics lover last updated on 26/Oct/17

Commented by math solver last updated on 26/Oct/17

Commented by Physics lover last updated on 26/Oct/17

Commented by Physics lover last updated on 26/Oct/17

Commented by Physics lover last updated on 26/Oct/17

Answered by ajfour last updated on 26/Oct/17
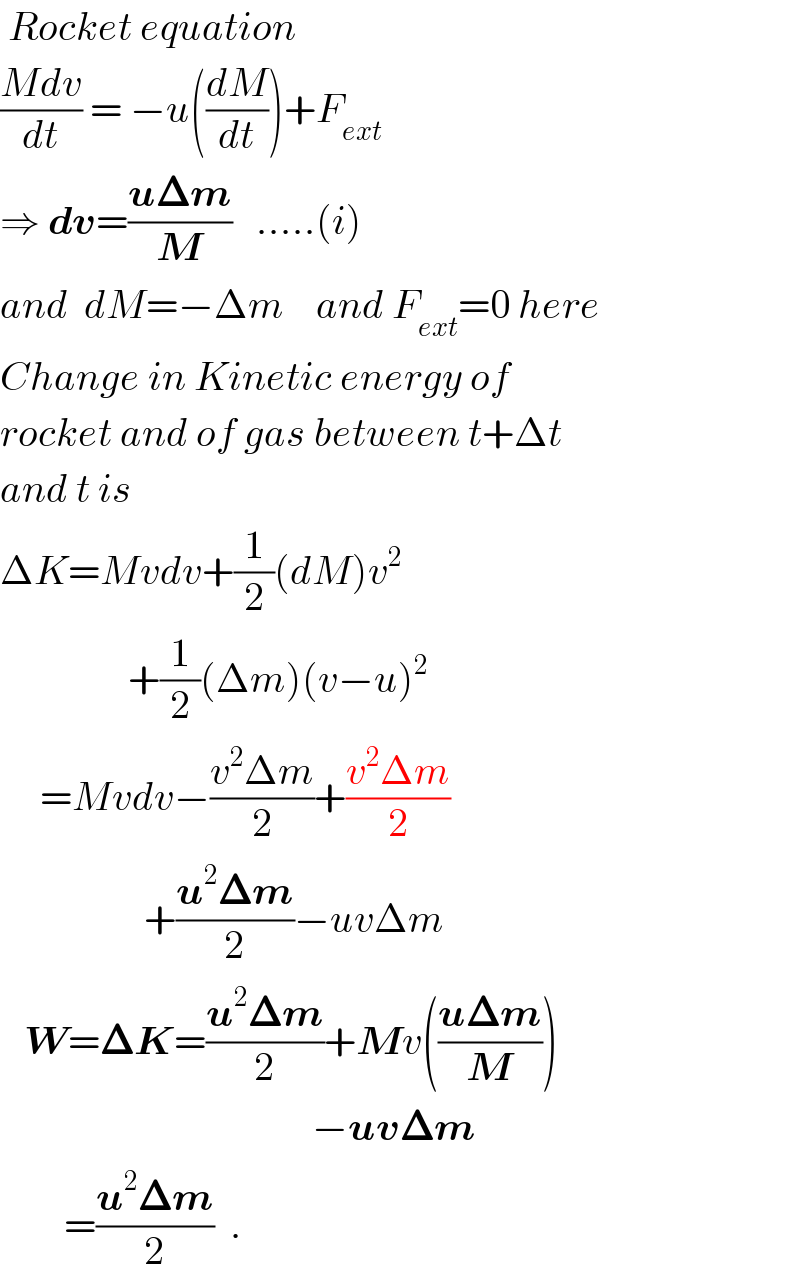
Commented by Tinkutara last updated on 26/Oct/17

