Question Number 117594 by mathdave last updated on 12/Oct/20

$${A}\:{rope}\:\mathrm{5}{m}\:{long}\:{is}\:{fastened}\:{to}\:{two}\:{hooks}\: \\ $$$$\mathrm{4}.\mathrm{0}{m}\:{apart}\:{on}\:{a}\:{horizontal} \\ $$$${ceiling}.{to}\:{the}\:{rope}\:{is}\:{attached}\:{a}\:\mathrm{10}{kg}\: \\ $$$${mass}\:{so}\:{that}\:{the}\:{segments}\:{of}\:{the}\:{rope} \\ $$$${are}\:\mathrm{3}.\mathrm{0}{m}\:{and}\:\mathrm{2}.\mathrm{0}{m}.{compute}\:{the} \\ $$$${tensionin}\:{each}\:{segment} \\ $$
Answered by mr W last updated on 12/Oct/20

Commented by mr W last updated on 12/Oct/20
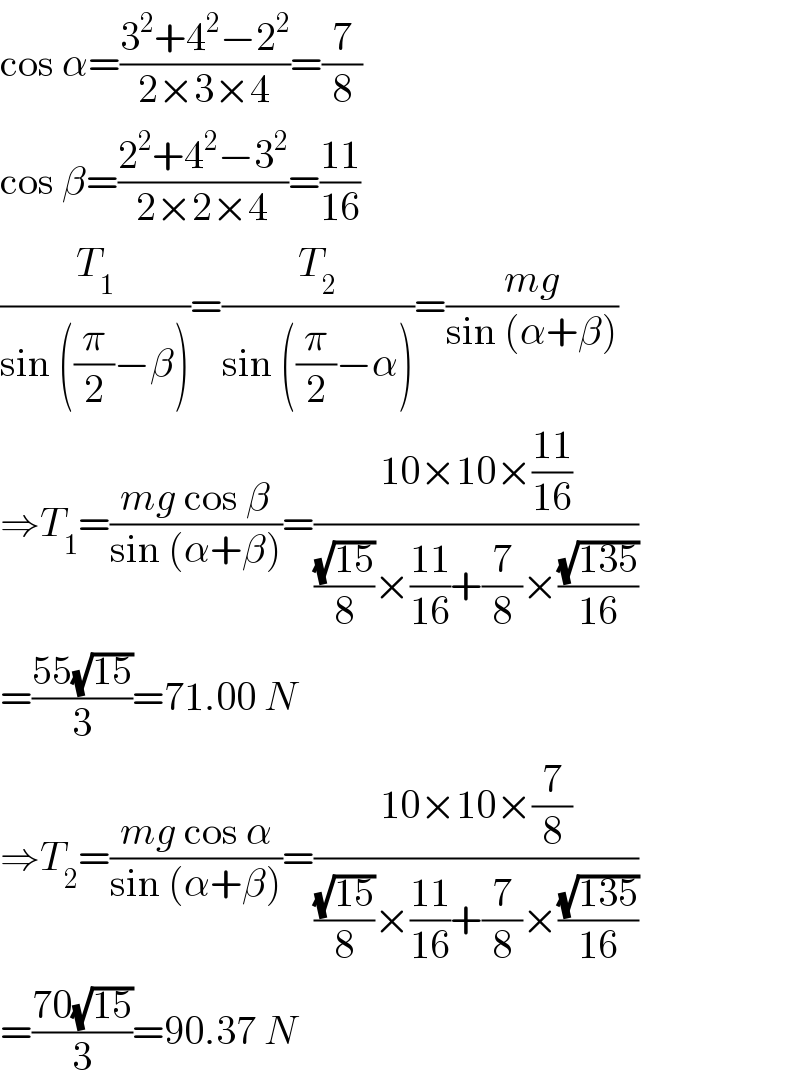
$$\mathrm{cos}\:\alpha=\frac{\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }{\mathrm{2}×\mathrm{3}×\mathrm{4}}=\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}×\mathrm{4}}=\frac{\mathrm{11}}{\mathrm{16}} \\ $$$$\frac{{T}_{\mathrm{1}} }{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\beta\right)}=\frac{{T}_{\mathrm{2}} }{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\alpha\right)}=\frac{{mg}}{\mathrm{sin}\:\left(\alpha+\beta\right)} \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\frac{{mg}\:\mathrm{cos}\:\beta}{\mathrm{sin}\:\left(\alpha+\beta\right)}=\frac{\mathrm{10}×\mathrm{10}×\frac{\mathrm{11}}{\mathrm{16}}}{\frac{\sqrt{\mathrm{15}}}{\mathrm{8}}×\frac{\mathrm{11}}{\mathrm{16}}+\frac{\mathrm{7}}{\mathrm{8}}×\frac{\sqrt{\mathrm{135}}}{\mathrm{16}}} \\ $$$$=\frac{\mathrm{55}\sqrt{\mathrm{15}}}{\mathrm{3}}=\mathrm{71}.\mathrm{00}\:{N} \\ $$$$\Rightarrow{T}_{\mathrm{2}} =\frac{{mg}\:\mathrm{cos}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)}=\frac{\mathrm{10}×\mathrm{10}×\frac{\mathrm{7}}{\mathrm{8}}}{\frac{\sqrt{\mathrm{15}}}{\mathrm{8}}×\frac{\mathrm{11}}{\mathrm{16}}+\frac{\mathrm{7}}{\mathrm{8}}×\frac{\sqrt{\mathrm{135}}}{\mathrm{16}}} \\ $$$$=\frac{\mathrm{70}\sqrt{\mathrm{15}}}{\mathrm{3}}=\mathrm{90}.\mathrm{37}\:{N} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
